Heading

In de echte wereld volgen oscillaties zelden de echte SHM. Door een of andere wrijving wordt de beweging meestal gedempt, zodat ze wegsterft, of meer kracht nodig heeft om door te gaan. In dit hoofdstuk bekijken we enkele voorbeelden van gedempte harmonische beweging en zien we hoe we de bewegingsvergelijkingen kunnen aanpassen om dit meer algemene geval te beschrijven.

Een gitaarsnaar stopt met oscilleren een paar seconden nadat er op is getokkeld. Om te blijven schommelen op een schommel in een speeltuin, moet je blijven duwen ((Figuur)). Hoewel we wrijving en andere niet-conservatieve krachten vaak klein of verwaarloosbaar kunnen maken, is een volledig ongedempte beweging zeldzaam. Het kan zelfs zo zijn dat we oscillaties willen dempen, zoals met schokdempers in auto’s.

Figuur 15.24 Om dempende krachten tegen te gaan, moet je blijven pompen aan een schommel. (credit: Bob Mical)

(Figuur) toont een massa m bevestigd aan een veer met een krachtconstante k. De massa wordt opgeheven tot een positie {A}_{0} , de beginamplitude, en dan losgelaten. De massa oscilleert rond de evenwichtsstand in een vloeistof met viscositeit, maar de amplitude neemt bij elke oscillatie af. Voor een systeem met een kleine hoeveelheid demping zijn de periode en de frequentie constant en bijna gelijk aan die van de SHM, maar de amplitude neemt geleidelijk af zoals getoond. Dit gebeurt omdat de niet-conservatieve dempingskracht energie aan het systeem onttrekt, meestal in de vorm van thermische energie.

Figuur 15.25 Voor een massa op een veer die oscilleert in een viskeuze vloeistof blijft de periode constant, maar de amplitudes van de oscillaties nemen af als gevolg van de demping door de vloeistof.

Bekijk de krachten die op de massa werken. Merk op dat de enige bijdrage van het gewicht bestaat uit het veranderen van de evenwichtspositie, zoals eerder in het hoofdstuk is besproken. De netto kracht is dus gelijk aan de kracht van de veer en de dempingskracht ({F}_{D}) . Als de grootte van de snelheid klein is, wat betekent dat de massa langzaam schommelt, is de dempingskracht evenredig met de snelheid en werkt tegen de bewegingsrichting in ({F}_{D}=\text{-}bv) . De netto kracht op de massa is dus

Wanneer we dit schrijven als een differentiaalvergelijking in x, krijgen we

Om de oplossing van deze vergelijking te bepalen, bekijken we de grafiek van de positie versus de tijd die in (Figuur) is weergegeven. De kromme lijkt op een cosinuskromme die oscilleert in de omhullende van een exponentiële functie {A}_{0}{e}^{-}t} waarbij \alpha =\frac{b}{2m} . De oplossing is

Het blijft een oefening om te bewijzen dat dit inderdaad de oplossing is. Om te bewijzen dat het de juiste oplossing is, neemt men de eerste en tweede afgeleide met betrekking tot de tijd en substitueert men deze in (Figuur). Er wordt gevonden dat (Figuur) de oplossing is als

Bedenk dat de hoekfrequentie van een massa die SHM ondergaat, gelijk is aan de vierkantswortel van de krachtconstante gedeeld door de massa. Dit wordt vaak de natuurlijke hoekfrequentie genoemd, die wordt weergegeven als

De hoekfrequentie voor gedempte harmonische beweging wordt

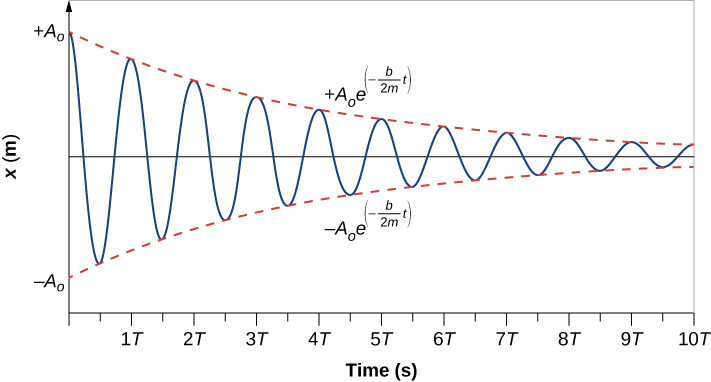
Figuur 15.26 Positie versus tijd voor de massa die oscilleert op een veer in een viskeuze vloeistof. Merk op dat de kromme een cosinusfunctie lijkt te zijn binnen een exponentiële omhullende.

Herinner je dat we, toen we deze beschrijving van gedempte harmonische beweging begonnen, stelden dat de demping klein moet zijn. Twee vragen komen bij me op. Waarom moet de demping klein zijn? En hoe klein is klein? Als je geleidelijk de hoeveelheid demping in een systeem verhoogt, beginnen de periode en de frequentie te worden beïnvloed, omdat demping de heen-en-weergaande beweging tegenwerkt en dus vertraagt. (De netto kracht is in beide richtingen kleiner.) Als de demping erg groot is, oscilleert het systeem niet eens, maar gaat het langzaam naar een evenwicht toe. De hoekfrequentie is gelijk aan

Als b groter wordt, wordt \frac{k}{m}-{(\frac{b}{2m})}^{2} kleiner en bereikt uiteindelijk nul als b=\sqrt{4mk} . Als b groter wordt, wordt \frac{k}{m}-{(\frac{b}{2m})}^{2} een negatief getal en is \sqrt{\frac{k}{m}-{(\frac{b}{2m})}^{2}} een complex getal.

(Figuur) toont de verplaatsing van een harmonische oscillator voor verschillende hoeveelheden demping. Als de dempingsconstante klein is, b<sqrt{4mk} oscilleert het systeem terwijl de amplitude van de beweging exponentieel afneemt. Men zegt dat dit systeem ondergedempt is, zoals in kromme (a). Veel systemen zijn ondergedempt, en oscilleren terwijl de amplitude exponentieel afneemt, zoals de massa die op een veer oscilleert. De demping kan vrij klein zijn, maar uiteindelijk komt de massa tot rust. Als de dempingsconstante b==sqrt{4mk} wordt het systeem kritisch gedempt genoemd, zoals in kromme (b). Een voorbeeld van een kritisch gedempt systeem zijn de schokbrekers in een auto. Het is gunstig dat de oscillaties zo snel mogelijk afnemen. Hier oscilleert het systeem niet, maar nadert het asymptotisch zo snel mogelijk de evenwichtstoestand. Curve (c) in (figuur) stelt een overgedempt systeem voor waarbij b>\sqrt{4mk}. Een overgedempt systeem zal over een langere periode een evenwicht benaderen.

Figuur 15.27 De positie versus tijd voor drie systemen bestaande uit een massa en een veer in een viskeuze vloeistof. (a) Als de demping klein is (b<\sqrt{4mk}), oscilleert de massa, waarbij de amplitude langzaam afneemt naarmate de energie door de niet-conservatieve kracht(en) wordt gedissipeerd. Het uiterste geval is (b) waar de demping (b=\sqrt{4mk}) is. (c) Als de demping zeer groot is (b>\sqrt{4mk}) , gaat de massa bij verplaatsing niet oscilleren, maar probeert terug te keren naar de evenwichtspositie.

Kritische demping is vaak gewenst, omdat zo’n systeem snel terugkeert naar het evenwicht en ook in evenwicht blijft. Bovendien brengt een constante kracht uitgeoefend op een kritisch gedempt systeem het systeem in de kortst mogelijke tijd naar een nieuwe evenwichtspositie zonder door te schieten of te oscilleren over de nieuwe positie.