Een verdeel en heers algoritme is een strategie om een groot probleem op te lossen door
- het probleem op te splitsen in kleinere deelproblemen
- de deelproblemen op te lossen, en
- ze te combineren om de gewenste uitkomst te krijgen.
Om het verdeel en heers algoritme te gebruiken, wordt recursie gebruikt. Leer meer over recursie in verschillende programmeertalen:
- Recursie in Java
- Recursie in Python
- Recursie in C++
Hoe werken verdeel en heers algoritmen?
Hier volgen de stappen:
- Versplitsen: Verdeel het gegeven probleem in deelproblemen met behulp van recursie.
- Overwin: Los de kleinere deelproblemen recursief op. Als het subprobleem klein genoeg is, los het dan direct op.
- Combineer: Combineer de oplossingen van de deelproblemen die deel uitmaken van het recursieve proces om het eigenlijke probleem op te lossen.
Laten we dit concept begrijpen met behulp van een voorbeeld.
Hier zullen we een array sorteren met behulp van de verdeel en heers aanpak (dwz.
- Laat de gegeven array zijn:

Array voor merge sort - Verdeel de array in twee helften.

Verdel de array in twee subdelen Verdeel elk subdeel recursief opnieuw in twee helften totdat je afzonderlijke elementen krijgt.
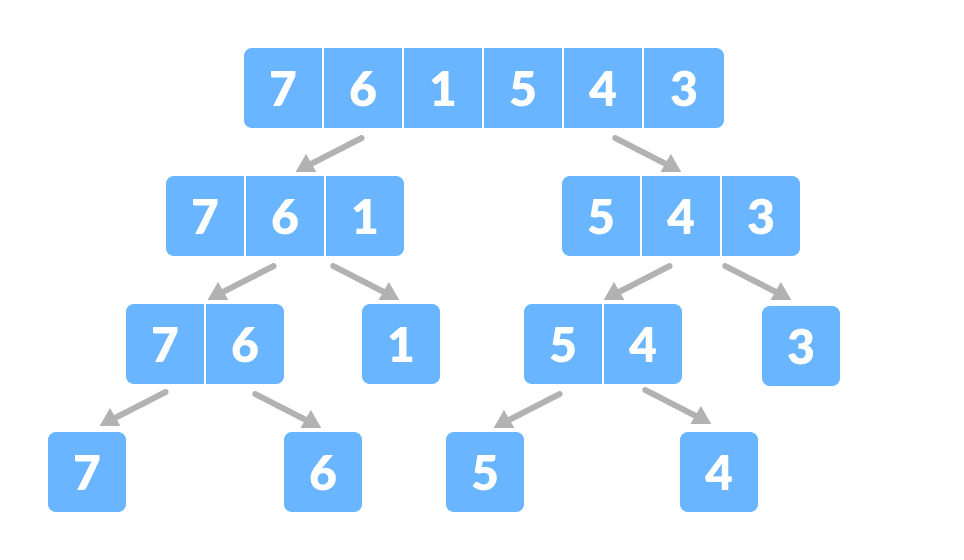
Verdeel de array in kleinere subdelen - Nu combineert u de afzonderlijke elementen op een gesorteerde manier. Hier gaan de stappen veroveren en combineren naast elkaar.
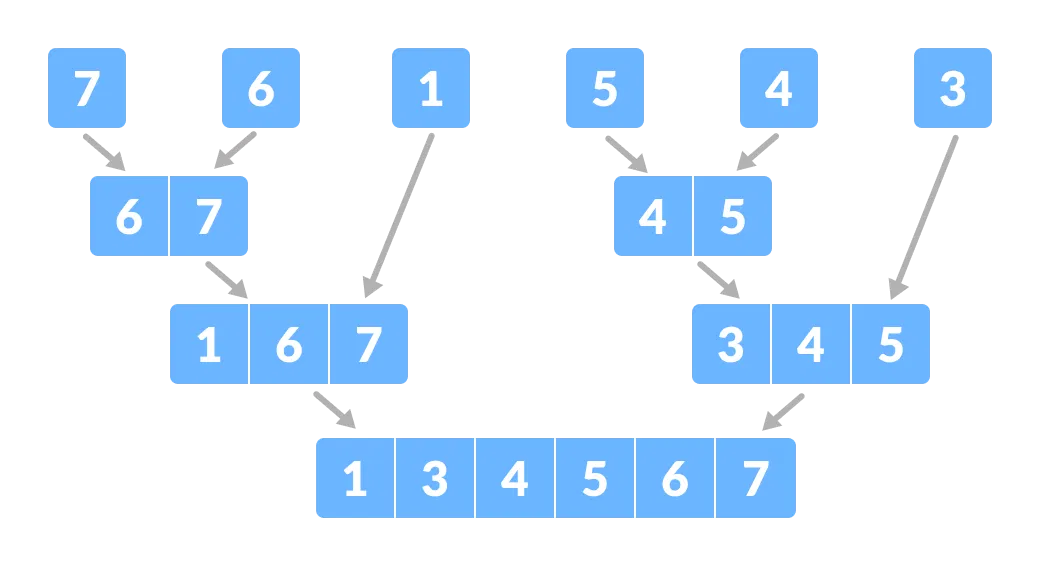
Combineer de subdelen
Tijdcomplexiteit
De complexiteit van het verdeel-en-heersalgoritme wordt berekend met behulp van de meestertheorema.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Laten we een voorbeeld nemen om de tijdcomplexiteit van een recursief probleem te vinden.
Voor een merge sort kan de vergelijking worden geschreven als:
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Divide and Conquer Vs Dynamic approach
De divide and conquer-aanpak verdeelt een probleem in kleinere deelproblemen; deze subproblemen worden verder recursief opgelost. Het resultaat van elk subprobleem wordt niet opgeslagen voor toekomstig gebruik, terwijl bij een dynamische aanpak het resultaat van elk subprobleem wordt opgeslagen voor toekomstig gebruik.
Gebruik de verdeel-en-heers-aanpak als hetzelfde subprobleem niet meerdere keren wordt opgelost. Gebruik de dynamische aanpak als het resultaat van een deelprobleem meerdere malen in de toekomst moet worden gebruikt.
Laten we dit met een voorbeeld begrijpen. Stel dat we proberen de Fibonaccireeks te vinden. Dan,
Verdel en heers aanpak:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Dynamische aanpak:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
In een dynamische aanpak slaat mem het resultaat van elk deelprobleem op.
Voordelen van het verdeel-en-heersalgoritme
- De complexiteit voor de vermenigvuldiging van twee matrices met de naïeve methode is O(n3), terwijl die met de verdeel-en-heers-benadering (d.w.z. de matrixvermenigvuldiging van Strassen) O(n2,8074) is. Deze aanpak vereenvoudigt ook andere problemen, zoals de Toren van Hanoi.
- Deze aanpak is geschikt voor multiprocessing systemen.
- Het maakt efficiënt gebruik van geheugencaches.
Verdeel en heers toepassingen
- Binary Search
- Merge Sort
- Quick Sort
- Strassen’s Matrix multiplication
- Karatsuba Algorithm



