Heading

Nel mio primo post sulle reti neurali, ho discusso un modello di rappresentazione per le reti neurali e come possiamo inserire degli input e calcolare un output. Abbiamo calcolato questo output, strato per strato, combinando gli input dallo strato precedente con i pesi per ogni connessione neurone-neurone. Ho detto che avremmo parlato di come trovare i pesi corretti per connettere i neuroni tra loro in un post futuro – questo è quel post!

Panoramica

Nel post precedente avevo dato per scontato che avessimo una magica conoscenza preliminare dei pesi corretti per ogni rete neurale. In questo post, capiremo effettivamente come far sì che la nostra rete neurale “impari” i pesi corretti. Tuttavia, per avere un punto di partenza, inizializziamo ciascuno dei pesi con valori casuali come ipotesi iniziale. Torneremo a rivedere questo passo di inizializzazione casuale più avanti nel post.

Dati i nostri pesi inizializzati a caso che collegano ciascuno dei neuroni, possiamo ora inserire la nostra matrice di osservazioni e calcolare le uscite della nostra rete neurale. Questo si chiama propagazione in avanti. Dato che abbiamo scelto i nostri pesi a caso, il nostro output probabilmente non sarà molto buono rispetto all’output previsto per il dataset.

Dove andiamo da qui?

Beh, per cominciare, definiamo cosa sia un “buon” output. Vale a dire, svilupperemo una funzione di costo che penalizza gli output lontani dal valore atteso.

In seguito, dobbiamo trovare un modo per cambiare i pesi in modo che la funzione di costo migliori. Qualsiasi percorso dato da un neurone di ingresso a un neurone di uscita è essenzialmente solo una composizione di funzioni; come tale, possiamo usare le derivate parziali e la regola della catena per definire la relazione tra qualsiasi peso dato e la funzione di costo. Possiamo usare questa conoscenza per sfruttare la discesa del gradiente nell’aggiornamento di ciascuno dei pesi.

Pre-requisiti

Quando stavo imparando la backpropagation, molte persone hanno cercato di astrarre la matematica sottostante (catene di derivate) e non sono mai stato veramente in grado di capire cosa diavolo stesse succedendo fino a quando ho visto la lezione del professor Winston al MIT. Spero che questo post dia una migliore comprensione della backpropagation rispetto al semplice “questo è il passo in cui inviamo l’errore all’indietro per aggiornare i pesi”.

Per afferrare pienamente i concetti discussi in questo post, dovreste avere familiarità con quanto segue:

Derivate parziali
Questo post sarà un po’ denso con molte derivate parziali. Tuttavia, è mia speranza che anche un lettore senza una precedente conoscenza del calcolo multivariato possa ancora seguire la logica dietro la backpropagation.

Se non avete familiarità con il calcolo, $frac{{{parziale f\sinistra( x \destra)}}{{{parziale x}}$ probabilmente vi sembrerà piuttosto estraneo. Puoi interpretare questa espressione come “come cambia $f\left( x \destra)$ quando cambio $x$? Questo sarà utile perché possiamo fare domande come “Come cambia la funzione di costo quando cambio questo parametro? Aumenta o diminuisce la funzione di costo?” alla ricerca dei parametri ottimali.

Se volete ripassare il calcolo multivariato, date un’occhiata alle lezioni di Khan Academy sull’argomento.

Discesa a gradiente
Per evitare che questo post diventi troppo lungo, ho separato l’argomento della discesa a gradiente in un altro post. Se non hai familiarità con il metodo, assicurati di leggerlo qui e di capirlo prima di continuare questo post.

Moltiplicazione della matrice
Qui c’è un rapido ripasso da Khan Academy.

Partiamo dal semplice

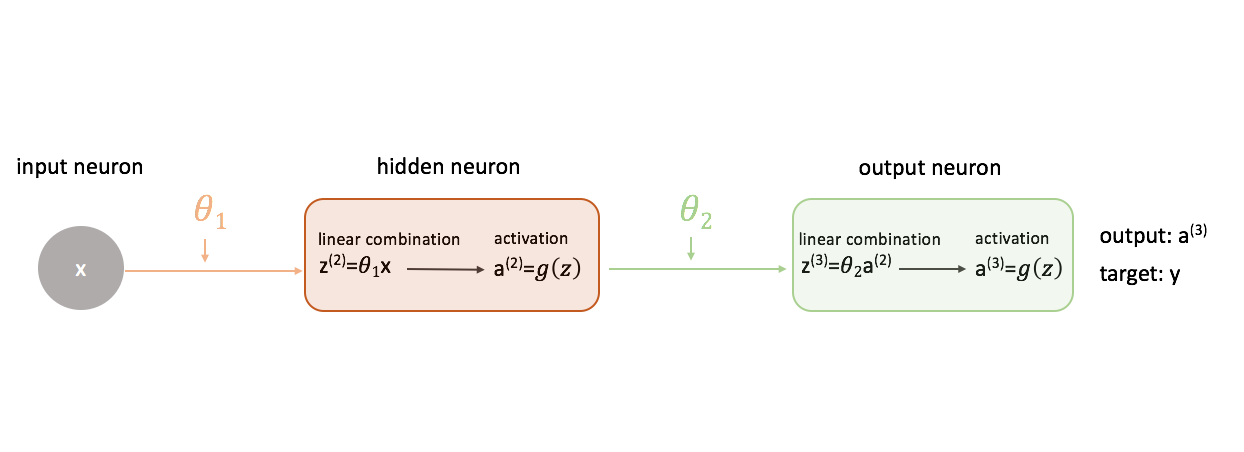
Per capire come usare la discesa del gradiente nell’addestramento di una rete neurale, iniziamo con la rete neurale più semplice: un neurone di ingresso, un neurone di livello nascosto e un neurone di uscita.

Per mostrare un quadro più completo di quello che sta succedendo, ho espanso ogni neurone per mostrare 1) la combinazione lineare di ingressi e pesi e 2) l’attivazione di questa combinazione lineare. È facile vedere che la fase di propagazione in avanti è semplicemente una serie di funzioni in cui l’output di una alimenta l’input della successiva.

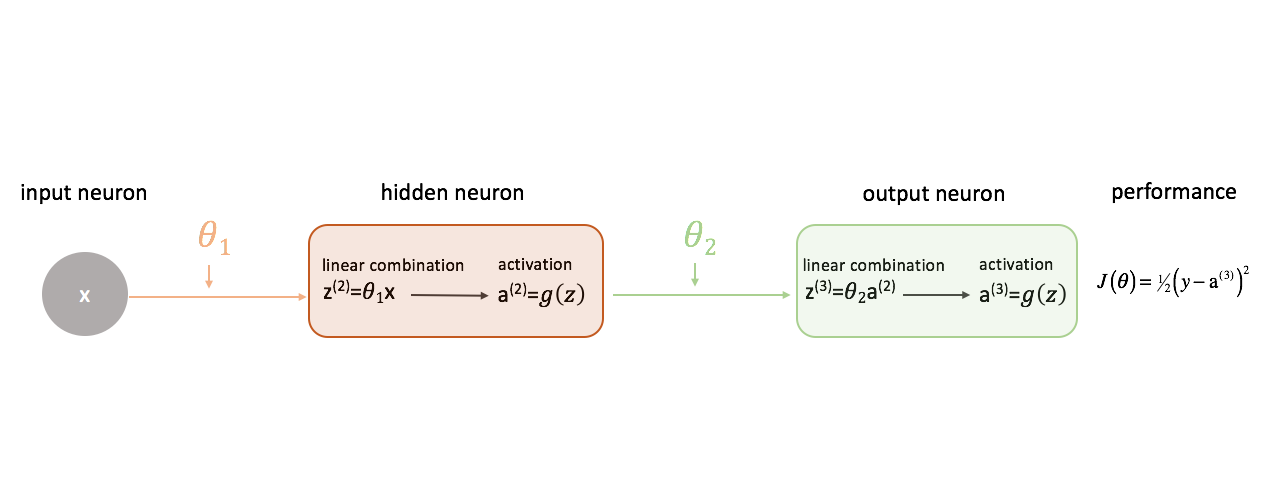
Definizione di “buone” prestazioni in una rete neurale

Definiamo la nostra funzione di costo semplicemente come l’errore al quadrato.

C’è una miriade di funzioni di costo che potremmo usare, ma per questa rete neurale l’errore al quadrato andrà benissimo.

Ricordo che vogliamo valutare l’output del nostro modello rispetto all’output di destinazione nel tentativo di minimizzare la differenza tra i due.

Relazione dei pesi alla funzione di costo

Per minimizzare la differenza tra l’output della nostra rete neurale e l’output di destinazione, abbiamo bisogno di sapere come cambia la performance del modello rispetto ad ogni parametro del nostro modello. In altre parole, dobbiamo definire la relazione (leggi: derivata parziale) tra la nostra funzione di costo e ogni peso. Possiamo quindi aggiornare questi pesi in un processo iterativo usando la discesa del gradiente.

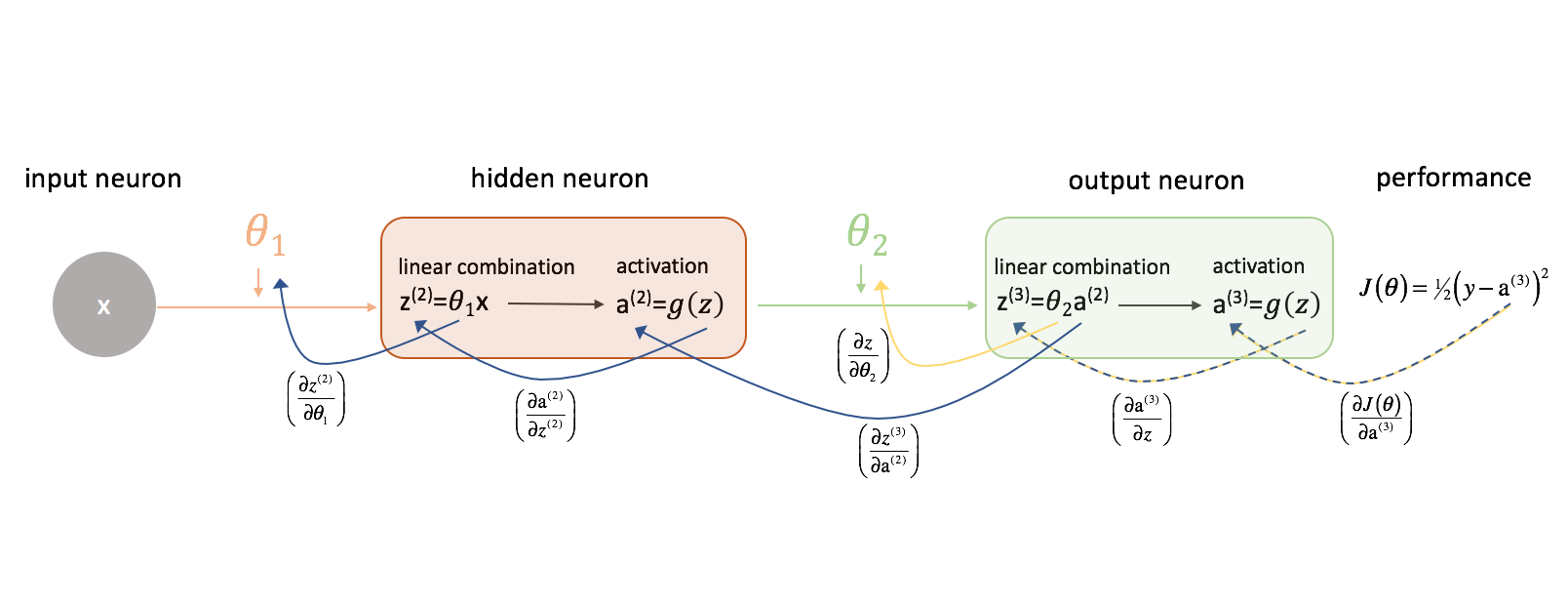
Guardiamo prima $frac{{parziale J\left( \theta \right)}}}{{parziale {\theta _2}}}. Tenete a mente la seguente figura mentre procediamo.

Prendiamoci un momento per esaminare come potremmo esprimere la relazione tra $J\left( \theta \right)$ e $\theta _2$. Notate come $ \theta _2$ è un input per ${z^{(3)}}$, che è un input per ${{rm{a}}^{(3)}}$, che è un input per $J\left( \theta \right)$. Quando cerchiamo di calcolare una derivata di questo tipo, possiamo usare la regola della catena per risolvere.

Come promemoria, la regola della catena afferma:

Applichiamo la regola della catena per risolvere per $\frac{{parziale di J\left( \theta \right)}}}{{parziale di {\theta _2}}.

Con una logica simile, possiamo trovare $frac{{parziale J\left( \theta \right)}}}{parziale {\theta _1}}$.

Per maggiore chiarezza, ho aggiornato il nostro diagramma della rete neurale per visualizzare queste catene. Assicuratevi di essere a vostro agio con questo processo prima di procedere.

Aggiungere complessità

Ora proviamo questo stesso approccio su un esempio leggermente più complicato. Ora, guarderemo una rete neurale con due neuroni nel nostro strato di input, due neuroni in uno strato nascosto e due neuroni nel nostro strato di output. Per ora, non terremo conto dei neuroni di polarizzazione che mancano negli strati di ingresso e nascosto.

Prendiamoci un secondo per ripassare la notazione che userò in modo che possiate seguire questi diagrammi. L’apice (1) denota in quale strato si trova l’oggetto e il pedice denota a quale neurone ci si riferisce in un dato strato. Per esempio $a_1^{(2)}$ è l’attivazione del primo neurone nel secondo strato. Per i valori dei parametri $\theta$, mi piace leggerli come un’etichetta postale – il primo valore denota a quale neurone l’input viene inviato nello strato successivo, e il secondo valore denota da quale neurone l’informazione viene inviata. Per esempio, ${theta _{21}^{(2)}}$ è usato per inviare l’input al 2° neurone, dal 1° neurone dello strato 2. L’apice che denota lo strato corrisponde alla provenienza dell’input. Questa notazione è coerente con la rappresentazione a matrice che abbiamo discusso nel mio post sulla rappresentazione delle reti neurali.

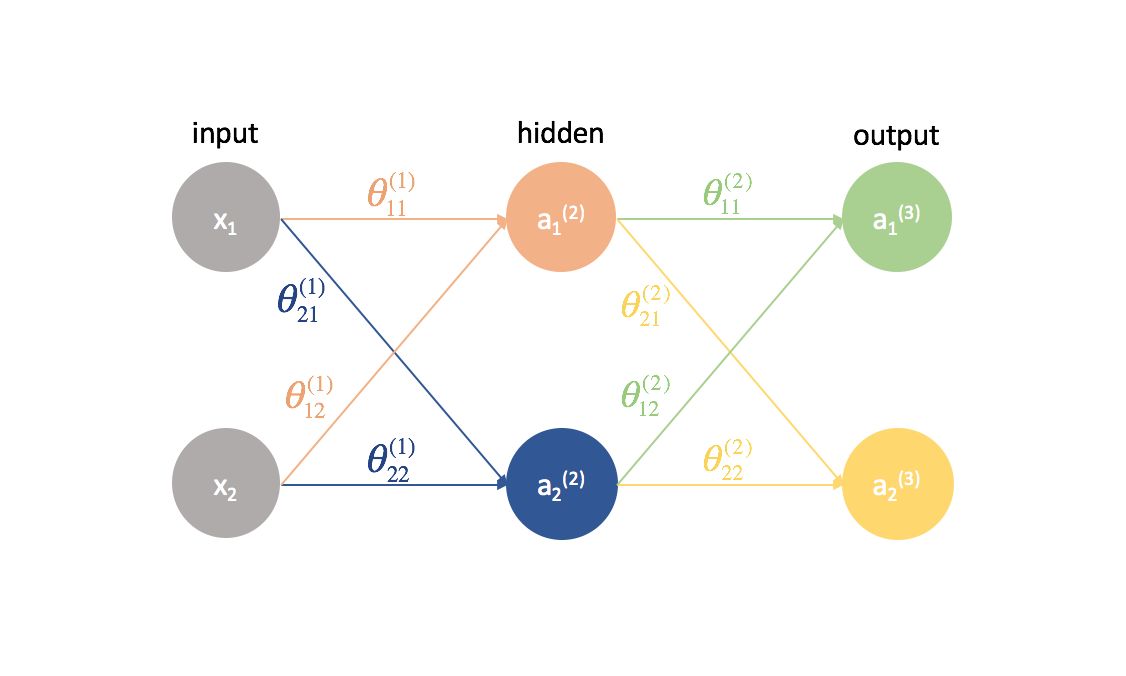
Espandiamo questa rete per esporre tutta la matematica che sta succedendo.

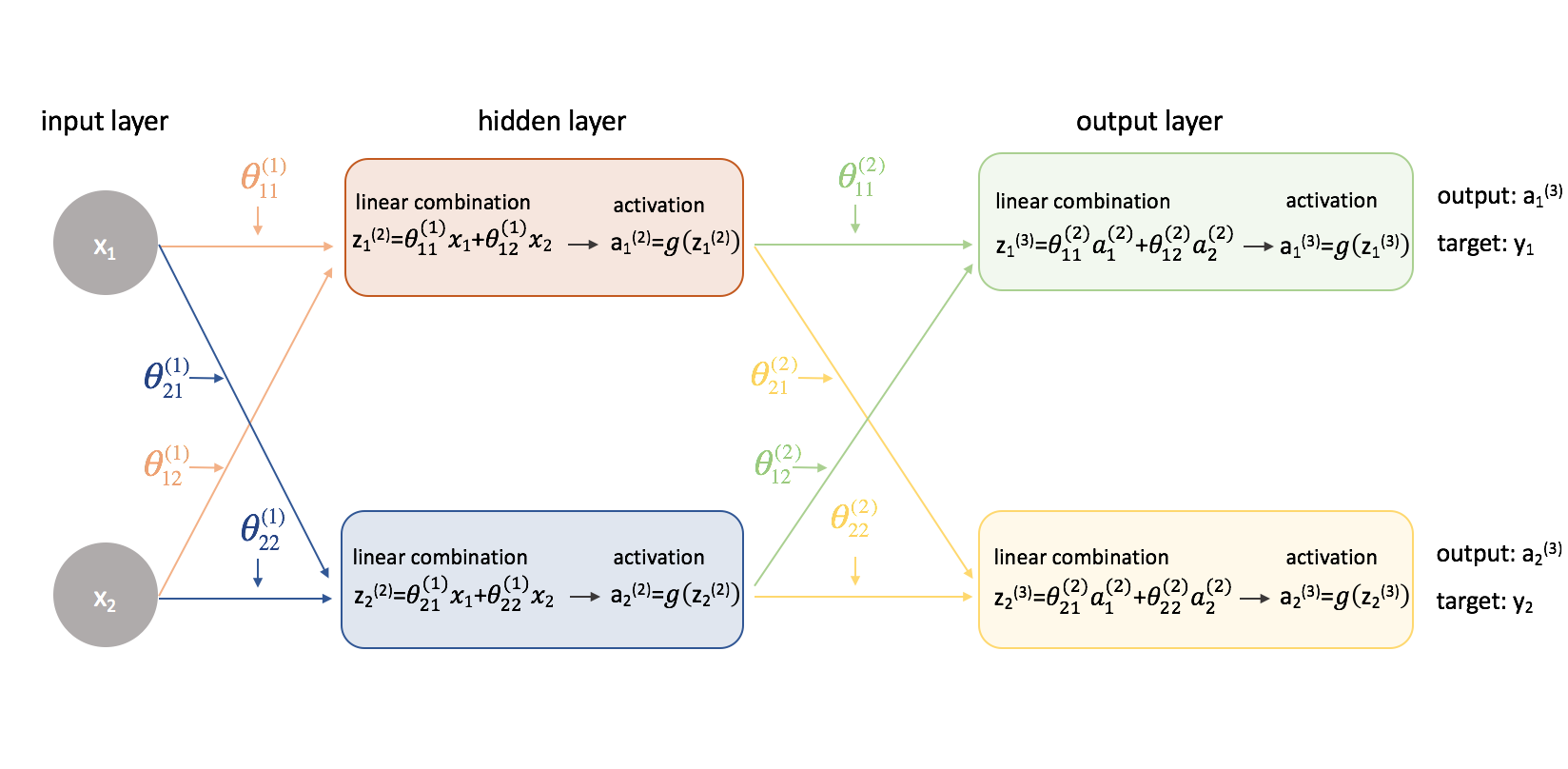
Ecco! Le cose sono diventate un po’ più complicate. Vi illustrerò il processo per trovare una delle derivate parziali della funzione di costo rispetto a uno dei valori dei parametri; lascerò il resto dei calcoli come esercizio per il lettore (e posterò i risultati finali qui sotto).

Prima di tutto, dovremo rivedere la nostra funzione di costo ora che abbiamo a che fare con una rete neurale con più di un output. Usiamo ora l’errore quadratico medio come nostra funzione di costo.

Nota: Se vi state allenando su osservazioni multiple (cosa che farete sempre nella pratica), avremo anche bisogno di eseguire una somma della funzione di costo su tutti gli esempi di allenamento. Per questa funzione di costo, è comune normalizzare per $\frac{1}{{m}}$ dove $m$ è il numero di esempi nel vostro dataset di allenamento.

Ora che abbiamo corretto la nostra funzione di costo, possiamo guardare come cambiare un parametro influenza la funzione di costo. In particolare, in questo esempio calcolerò $frac{{parziale J\left( \theta \right)}}}{parziale \theta _{11}^{(1)}}$. Guardando il diagramma, $ {theta _{11}^{(1)}$ influenza l’uscita sia per $a _1^{(3)}$ che per $a _2^{(3)}$. Poiché la nostra funzione di costo è una somma di costi individuali per ogni uscita, possiamo calcolare la catena di derivazione per ogni percorso e semplicemente sommarli.

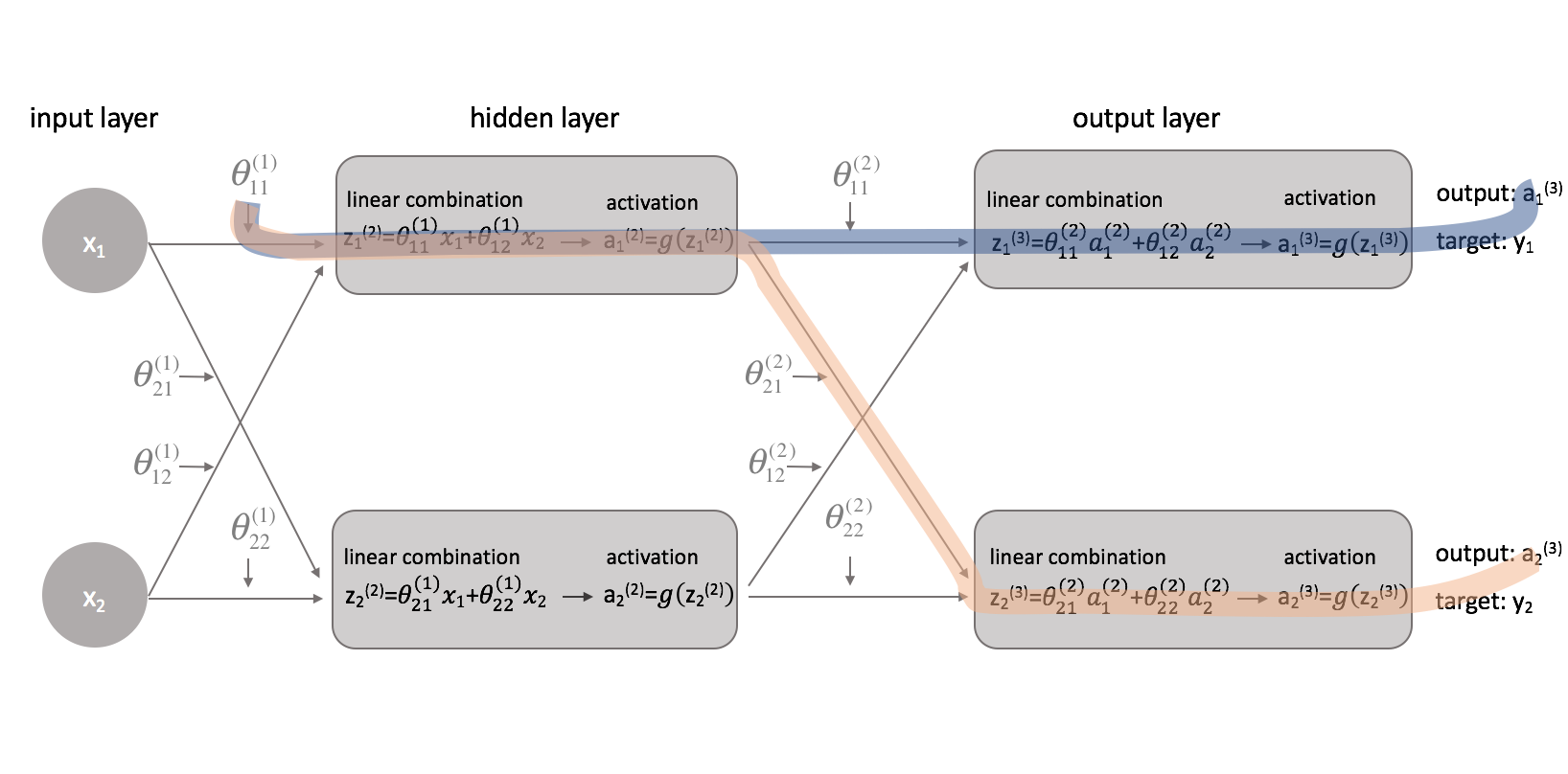
La catena di derivazione per il percorso blu è:
$ \sinistra( {\frac{{parziale J\left( \theta \destra)}{{parziale {\rm{a}} _1^{(3)}}}} dx)\sinistra(\frac)\sinistra(\frac)\parziale di \rm{a} _1^{(3)}}}{parziale z _1^{(3)}}}} \dx)\sinistra( {frac{partial z _1^{(3)}}{partial z _1^{(3)}}{partial z _1^{(3)}} _1^{(2)}}}} \dx)\sinistra( {frac{{parziale di z _1^{(3)} _1^{(2)}}}{parziale z _1^{(2)}}}} \destra)\sinistra( {frac {parziale z _1^{(2)}}}{parziale \theta _{11}^{(1)}}}} \destra) $

La catena delle derivate per il percorso arancione è:
$ \sinistra( {frac{{parziale J\left( \theta \destra)}}}{parziale {rm{a}} _2^{(3)}}}} dx)\sinistra(\frac)\sinistra(\frac)\parziale di \rm{a} _2^{(3)}}}{{parziale z _2^{(3)}}}} \dx)\sinistra( {frac{{parziale z _2^{(3)}}{parziale z _2^{(3)}}{parziale z _rm{a}} _1^{(2)}}}} \dx)\sinistra( {frac{{parziale di z _2^{(3)} _1^{(2)}}}{parziale z _1^{(2)}}}} \destra)\sinistra( {frac{parziale z _1^{(2)}}}{parziale \theta _{11}^{(1)}}}} \destra)$

Combinando questi, otteniamo l’espressione totale per $\frac{{parziale J\left( \theta \destra)}}{parziale \theta _{11}^{(1)}}$.

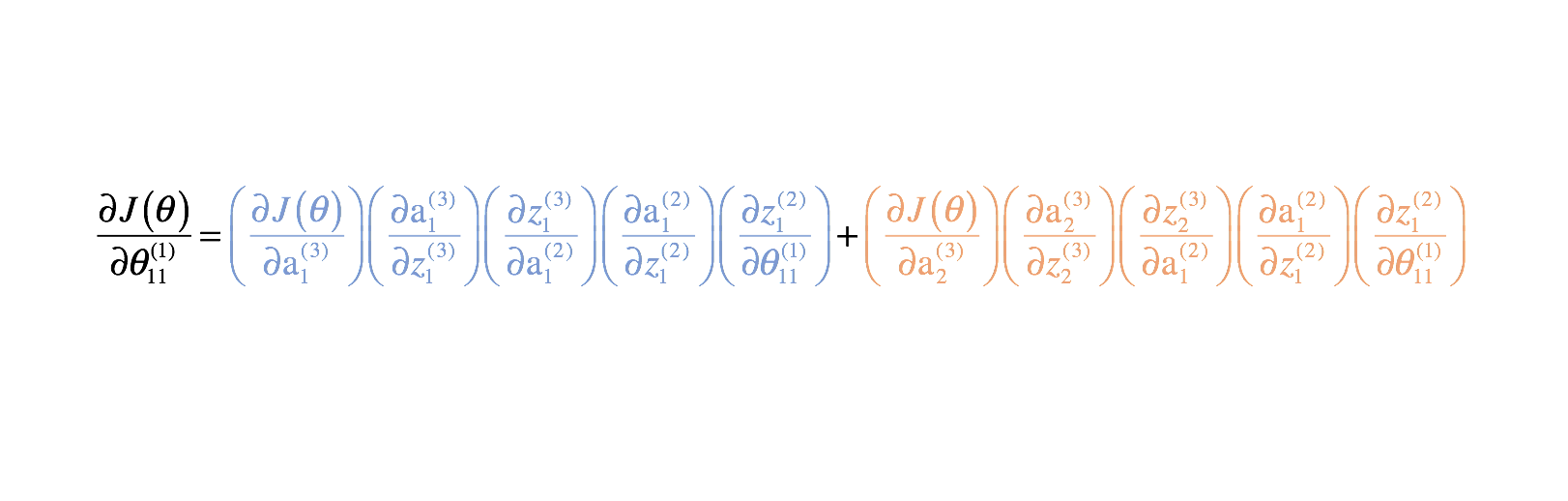
Ho fornito il resto delle derivate parziali sotto. Ricordate, abbiamo bisogno di queste derivate parziali perché descrivono come il cambiamento di ogni parametro influenza la funzione di costo. Così, possiamo usare questa conoscenza per cambiare tutti i valori dei parametri in un modo che continua a diminuire la funzione di costo fino a quando non convergiamo su qualche valore minimo.

Parametri del livello 2

Parametri del livello 1

Woah là. Siamo appena passati da una rete neurale con 2 parametri che aveva bisogno di 8 termini di derivazione parziale nell’esempio precedente a una rete neurale con 8 parametri che aveva bisogno di 52 termini di derivazione parziale. Questo ci sfuggirà rapidamente di mano, specialmente considerando che molte reti neurali usate in pratica sono molto più grandi di questi esempi.

Fortunatamente, ad un esame più attento molte di queste derivate parziali si ripetono. Se siamo intelligenti su come approcciare questo problema, possiamo ridurre drasticamente il costo computazionale dell’addestramento. Inoltre, sarebbe davvero una rottura se dovessimo calcolare manualmente le catene di derivate per ogni parametro. Guardiamo cosa abbiamo fatto finora e vediamo se possiamo generalizzare un metodo per questa follia.

Generalizzare un metodo

Esaminiamo le derivate parziali di cui sopra e facciamo alcune osservazioni. Inizieremo con l’esaminare le derivate parziali rispetto ai parametri del livello 2. Ricordate, i parametri dello strato 2 sono combinati con le attivazioni dello strato 2 per alimentare come input lo strato 3.

Parametri dello strato 2

Analizziamo le seguenti espressioni; vi incoraggio a risolvere le derivate parziali man mano che procediamo per convincervi della mia logica.

In primo luogo, sembra che le colonne contengano valori molto simili. Per esempio, la prima colonna contiene le derivate parziali della funzione di costo rispetto alle uscite della rete neurale. In pratica, si tratta della differenza tra l’uscita prevista e l’uscita effettiva (e quindi scalata da $m$) per ciascuno dei neuroni di uscita.

La seconda colonna rappresenta la derivata della funzione di attivazione utilizzata nello strato di uscita. Si noti che per ogni strato, i neuroni useranno la stessa funzione di attivazione. Una funzione di attivazione omogenea all’interno di uno strato è necessaria per poter sfruttare le operazioni di matrice nel calcolo dell’uscita della rete neurale. Così, il valore per la seconda colonna sarà lo stesso per tutti e quattro i termini.

La prima e la seconda colonna possono essere combinate come $\delta _i^{(3)}$ per comodità in seguito. Non è immediatamente evidente il motivo per cui questo sarebbe utile, ma vedrete, andando indietro di un altro livello, perché questo è utile. Le persone si riferiranno spesso a questa espressione come il termine “errore” che usiamo per “rimandare indietro l’errore dall’uscita in tutta la rete”. Vedremo presto perché questo è il caso. Ogni neurone nella rete avrà un corrispondente termine $\delta$ che risolveremo.

La terza colonna rappresenta come il parametro di interesse cambia rispetto agli ingressi ponderati per lo strato corrente; quando si calcola la derivata questa corrisponde all’attivazione dallo strato precedente.

Vorrei anche notare che i primi due termini della derivata parziale sembrano riguardare il primo neurone di uscita (neurone 1 dello strato 3) mentre gli ultimi due termini della derivata parziale sembrano riguardare il secondo neurone di uscita (neurone 2 dello strato 3). Questo è evidente nel termine $frac{{parziale J\left( \theta \right)}}}{{parziale {\rm{a}}}_i^{(3)}}. Usiamo questa conoscenza per riscrivere le derivate parziali usando l’espressione $\delta$ che abbiamo definito sopra.

Prossimo, andiamo avanti e calcoliamo l’ultimo termine della derivata parziale. Come abbiamo notato, questa derivata parziale finisce per rappresentare le attivazioni dello strato precedente.

Nota: trovo utile usare il grafico della rete neurale espansa nella sezione precedente quando si calcolano le derivate parziali.

Sembra che stiamo combinando i termini di “errore” con le attivazioni dello strato precedente per calcolare ogni derivata parziale. È anche interessante notare che gli indici $j$ e $k$ per $\theta _{jk}$ corrispondono agli indici combinati di $\delta _j^{(3)}$ e ${rm{a}}}

Vediamo se possiamo trovare un’operazione matriciale per calcolare tutte le derivate parziali in una sola espressione.

${{delta ^{(3)}}$ è un vettore di lunghezza $j$ dove $j$ è uguale al numero di neuroni di uscita.

δ (3) = f ′ ( a (3) )

${rm{a}}^{(2)}$ è un vettore di lunghezza $k$ dove $k$ è il numero di neuroni nello strato precedente. I valori di questo vettore rappresentano le attivazioni dello strato precedente calcolate durante la propagazione in avanti; in altre parole, è il vettore degli ingressi allo strato di uscita.

$ {a^{(2)}}} = \left $

Moltiplicando insieme questi vettori, possiamo calcolare tutti i termini di derivazione parziale in un’unica espressione.

∂J( θ ) ∂ θ ij (2) ==

Per riassumere, vedi il grafico qui sotto.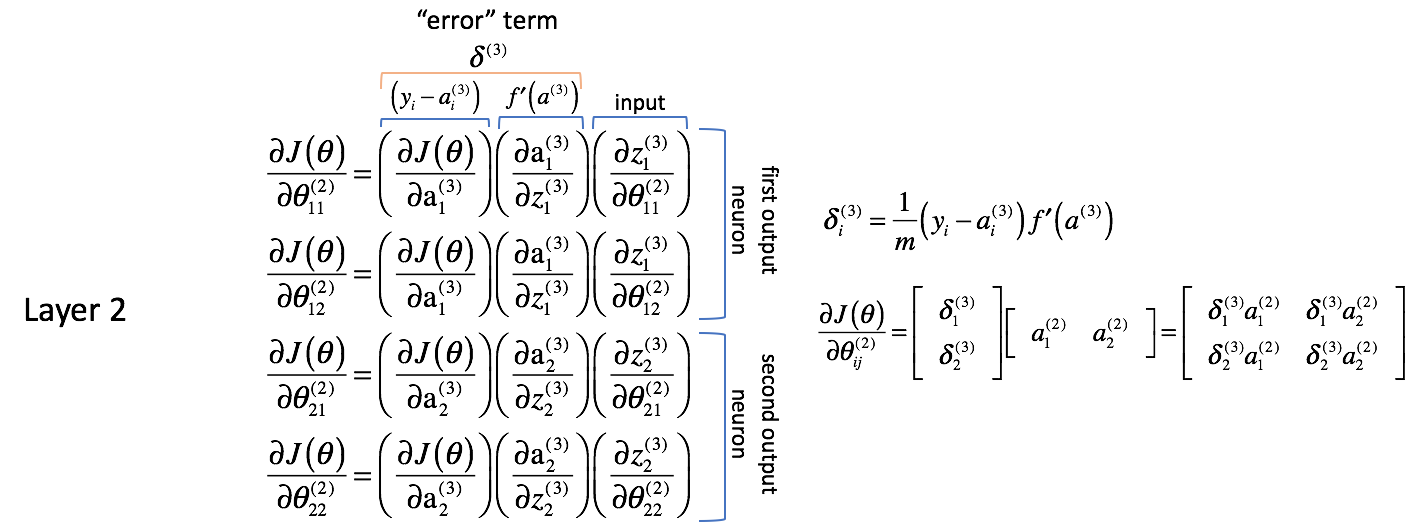

Nota: Tecnicamente, la prima colonna dovrebbe anche essere scalata per $m$ per essere una derivata precisa. Tuttavia, il mio obiettivo era quello di sottolineare che questa è la colonna in cui ci interessa la differenza tra i risultati attesi e quelli effettivi. Il termine $\delta$ sulla destra ha l’espressione della derivata completa.

Parametri del livello 1

Ora diamo un’occhiata e vediamo cosa sta succedendo nel livello 1.

Dove i pesi nel livello 2 influenzano direttamente solo un output, i pesi nel livello 1 influenzano tutti gli output. Ricordiamo il seguente grafico.

Questo risulta in una derivata parziale della funzione di costo rispetto a un parametro che ora diventa una sommatoria di diverse catene. In particolare, avremo una catena di derivate per ogni $\delta$ che abbiamo calcolato nel prossimo livello in avanti. Ricordate, siamo partiti dalla fine della rete e stiamo lavorando all’indietro attraverso la rete. Quindi, lo strato successivo rappresenta i valori di $\delta$ che abbiamo calcolato in precedenza.

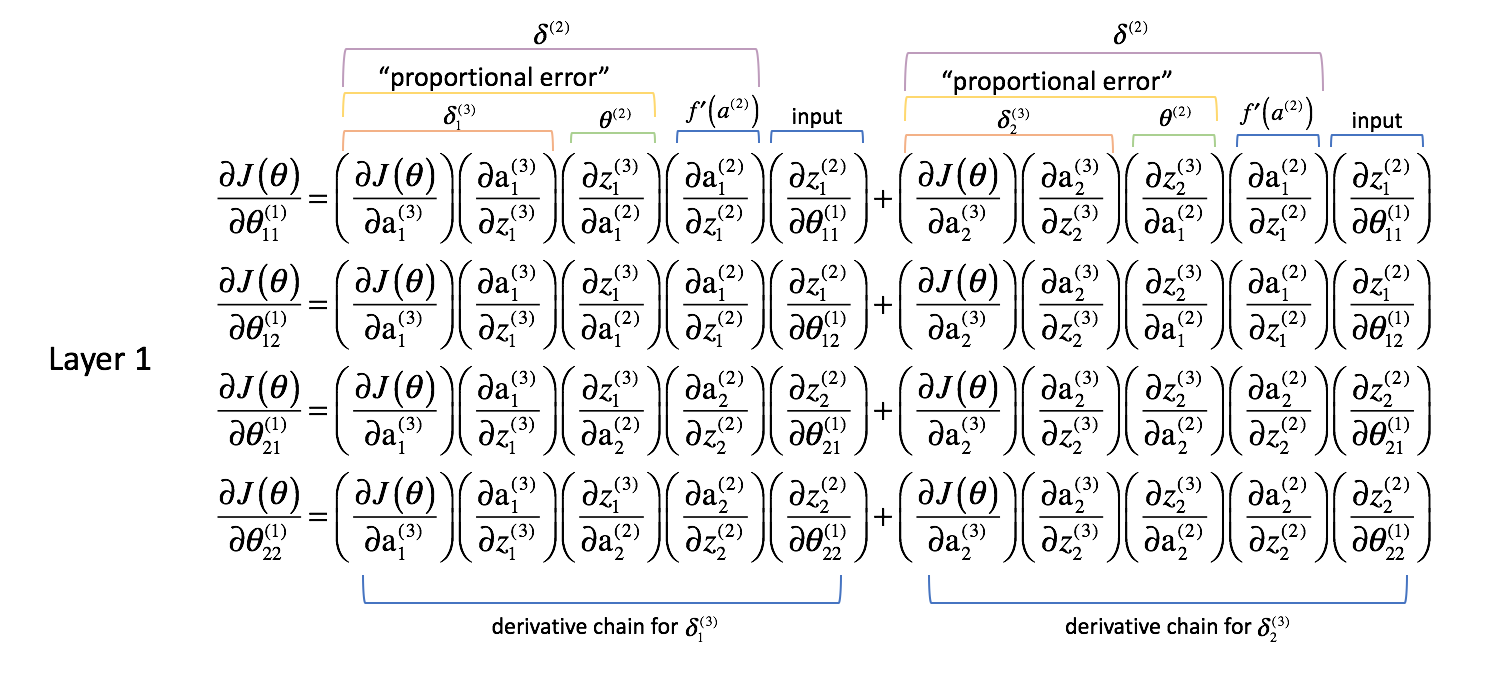
Come abbiamo fatto per lo strato 2, facciamo alcune osservazioni.

Le prime due colonne (di ogni termine sommato) corrispondono a un $\delta _j^{(3)}$ calcolato nello strato successivo (ricordate, siamo partiti dalla fine della rete e stiamo lavorando all’indietro).

La terza colonna corrisponde a qualche parametro che collega lo strato 2 allo strato 3. Se consideriamo $\delta _j^{(3)}$ come un termine di “errore” per lo strato 3, e ogni catena di derivazione è ora una somma di questi errori, allora questa terza colonna ci permette di pesare ogni rispettivo errore. Così, i primi tre termini combinati rappresentano una qualche misura dell’errore proporzionale.

Definiremo anche $\delta$ per tutti gli strati escluso lo strato di uscita per includere questa combinazione di errori ponderati.

$ \delta _j^{(l)} = f’\sinistra( {{a^{(l)}}} \destra)\somma_limiti _{i = 1}^n {\delta _i^{(l + 1)\theta _{ij}^{(l)} $

Potremmo scriverlo più succintamente usando espressioni matriciali.

$ {\delta ^{(l)}} = {\delta ^{(l + 1)}}{Theta ^{(l)}}f’\left( {{a^{(l)}}} \Destra) $

Nota: è la notazione standard per indicare i vettori con lettere minuscole e le matrici con lettere maiuscole. Così, $\theta$ rappresenta un vettore mentre $\Theta$ rappresenta una matrice.

La quarta colonna rappresenta la derivata della funzione di attivazione usata nello strato corrente. Ricorda che per ogni strato, i neuroni useranno la stessa funzione di attivazione.

Infine, la quinta colonna rappresenta vari input dallo strato precedente. In questo caso, sono gli input effettivi della rete neurale.

Diamo un’occhiata più da vicino a uno dei termini, $frac{{parziale J\left( \theta \right)}}}{{parziale \theta _{11}^{(1)}}}.

Infine, abbiamo stabilito che le prime due colonne di ogni catena di derivate sono state precedentemente calcolate come $\delta _j^{(3)}$.

$ \frac{{parziale J\left( \theta \right)}}}{parziale \theta _{11}^{(1)}} = \delta _1^{(3)}{ sinistra( {\frac{parziale z _1^{(3)}}{{parziale {\rm{a}} _1^{(2)}}}} \dx)\sinistra( {frac{{parziale di z _1^{(3)} _1^{(2)}}}{parziale z _1^{(2)}}}} \destra)\sinistra( \frac{parziale z _1^{(2)}}{parziale \theta _{11}^{(1)}}}} \dx) + \delta _2^{(3)}sinistra( {\frac{{parziale z _2^{(3)}}}{parziale {rm{a}} _1^{(2)}}}} \dx)\sinistra( {frac{{parziale di z _2^{(3)} _1^{(2)}}}{parziale z _1^{(2)}}}} \destra)\sinistra( {frac {parziale z _1^{(2)}}}{parziale \theta _{11}^{(1)}}}} \Destra) $

Inoltre, abbiamo stabilito che la terza colonna di ogni catena di derivate era un parametro che agiva per pesare ciascuno dei rispettivi termini $delta$. Abbiamo anche stabilito che la quarta colonna era la derivata della funzione di attivazione.

$ \frac{parziale J\left( \theta \right)}}{parziale \theta _{11}^{(1)}}} = \delta _1^{(3)}theta _{11}^{(2)}f’\left( {{a^{(2)}} \dx)\sinistra( \frac{parziale z _1^{(2)}{parziale \theta _{11}^{(1)}}}} \destra) + \delta _2^{(3)\theta _{21}^{(2)\f’\sinistra( {{a^{(2)} \destra)\sinistra(\frac{{parziale z _1^{(2)}{parziale \theta _{11}^{(1)}}}} \destra) $

Factoring out $\left( {\frac{{parziale z_1^{(2)}}}{parziale \theta _{11}^{(1)}}}} \destra)$,

$ \frac{{{parziale J\left( \theta \destra)}}{parziale \theta _{11}^{(1)}}} = \left( {frac{parziale z _1^{(2)}}{parziale \theta _{11}^{(1)}}}} \dx)\sinistra( delta _1^{(3)}theta _{11}^{(2)}f’\sinistra( {{a^{(2)} \destra) + \delta _2^{(3)}f’\delta _{21}^{(2)}f’\sinistra( {{a^{(2)} \Destra) $

ci rimane la nostra nuova definizione di $\delta_j^{(l)}$. Andiamo avanti e sostituiamola.

$ \frac{{parziale J\left( \theta \right)}}{parziale \theta _{11}^{(1)}} = \left( {\frac{parziale z _1^{(2)}}{parziale \theta _{11}^{(1)}}}} \destra)\sinistra( {delta _1^{(2)}

Infine, abbiamo stabilito che la quinta colonna (${frac{{parziale z_1^{(2)}}{parziale \theta_{11}^{(1)}}}}$) corrisponde ad un input dallo strato precedente. In questo caso, la derivata è calcolata per essere $x_1$.

$ \frac{{parziale J\left( \theta \right)}}{parziale \theta _{11}^{(1)}} = \delta _1^{(2)}{x _1} $

Ancora una volta troviamo un’operazione matrice per calcolare tutte le derivate parziali in una sola espressione.

$delta ^{(2)}$ è un vettore di lunghezza $j$ dove $j$ è il numero di neuroni nello strato corrente (strato 2). Possiamo calcolare $\delta ^{(2)}$ come la combinazione pesata degli errori dello strato 3, moltiplicata per la derivata della funzione di attivazione usata nello strato 2.

δ (2) = f ′ ( a (2) )=

$x$ è un vettore di valori di input.

Moltiplicando insieme questi vettori, possiamo calcolare tutti i termini di derivazione parziale in una sola espressione.

∂J( θ ) ∂ θ ij (1) ==

Se siete arrivati fin qui, complimenti! Abbiamo appena calcolato tutte le derivate parziali necessarie per usare la discesa del gradiente e ottimizzare i valori dei nostri parametri. Nella prossima sezione, introdurrò un modo per visualizzare il processo che abbiamo appena sviluppato, oltre a presentare un metodo end-to-end per implementare la backpropagation. Se avete capito tutto fino a questo punto, dovrebbe essere una navigazione tranquilla da qui in poi.

Backpropagation

Nell’ultima sezione, abbiamo sviluppato un modo per calcolare tutte le derivate parziali necessarie per la discesa del gradiente (derivata parziale della funzione di costo rispetto a tutti i parametri del modello) usando espressioni di matrice. Nel calcolare le derivate parziali, siamo partiti dalla fine della rete e, strato per strato, abbiamo lavorato a ritroso fino all’inizio. Abbiamo anche sviluppato un nuovo termine, $\delta$, che serve essenzialmente a rappresentare tutti i termini di derivazione parziale che avremmo bisogno di riutilizzare in seguito e procediamo, strato per strato, all’indietro attraverso la rete.

Nota: Backpropagation è semplicemente un metodo per calcolare la derivata parziale della funzione di costo rispetto a tutti i parametri. L’ottimizzazione effettiva dei parametri (addestramento) è fatta dalla discesa del gradiente o da un’altra tecnica di ottimizzazione più avanzata.

Generalmente, abbiamo stabilito che è possibile calcolare le derivate parziali per lo strato $l$ combinando i termini $\delta$ dello strato successivo in avanti con le attivazioni dello strato corrente.

$ \frac{{parziale J\left( \theta \right)}}}{parziale \theta _{ij}^{(l)}} = {{left( {{delta ^{(l + 1)}} \dx)^T}{a^{(l)}} $

Visualizzazione della backpropagation

Prima di definire il metodo formale per la backpropagation, vorrei fornire una visualizzazione del processo.

Prima di tutto, dobbiamo calcolare l’output di una rete neurale attraverso la propagazione in avanti.

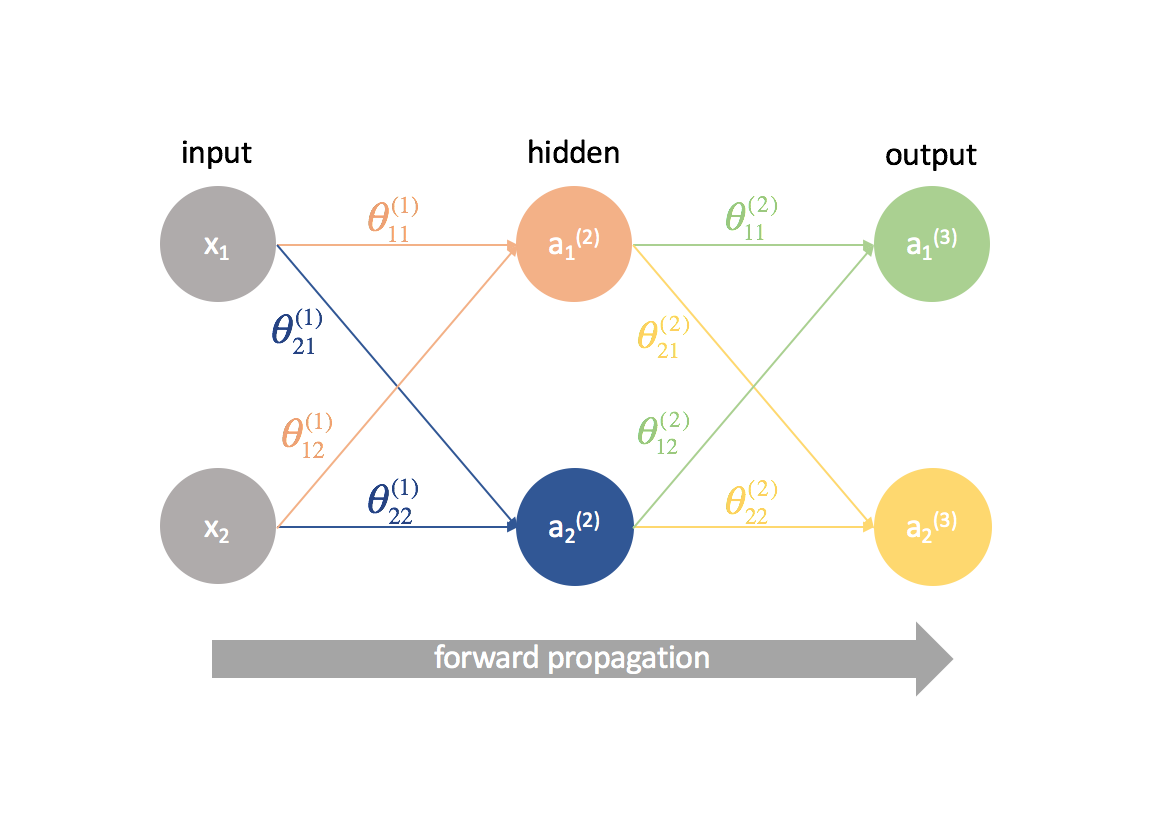
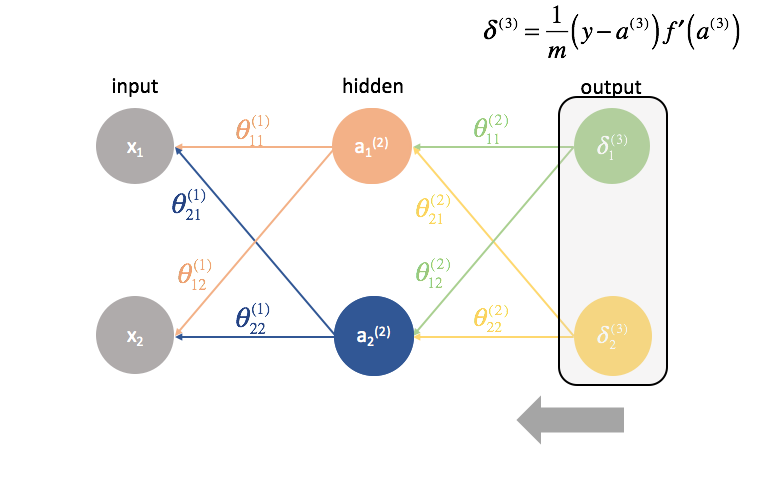
Dopo, calcoliamo i termini ${{delta ^{(3)}}$ per l’ultimo strato della rete. Ricordate, questi termini $\delta$ consistono in tutte le derivate parziali che saranno usate di nuovo nel calcolo dei parametri per gli strati più indietro. In pratica, ci riferiamo tipicamente a $\delta$ come termine di “errore”.

${{{Theta ^{(2)}}}$ è la matrice dei parametri che collega lo strato 2 al 3. Moltiplichiamo l’errore del terzo strato per gli ingressi del secondo strato per calcolare le nostre derivate parziali per questo insieme di parametri.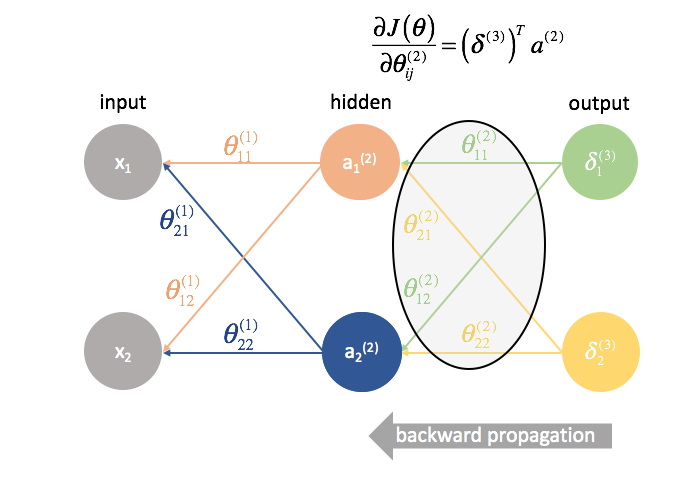

In seguito, “rimandiamo indietro” i termini di “errore” nello stesso identico modo in cui “mandiamo avanti” gli ingressi di una rete neurale. L’unica differenza è che questa volta, partiamo da dietro e alimentiamo un termine di errore, strato per strato, all’indietro attraverso la rete. Da qui il nome: backpropagation. L’atto di “rimandare indietro il nostro errore” è compiuto attraverso l’espressione ${{delta ^{(3)}}{{Theta ^{(2)}}$.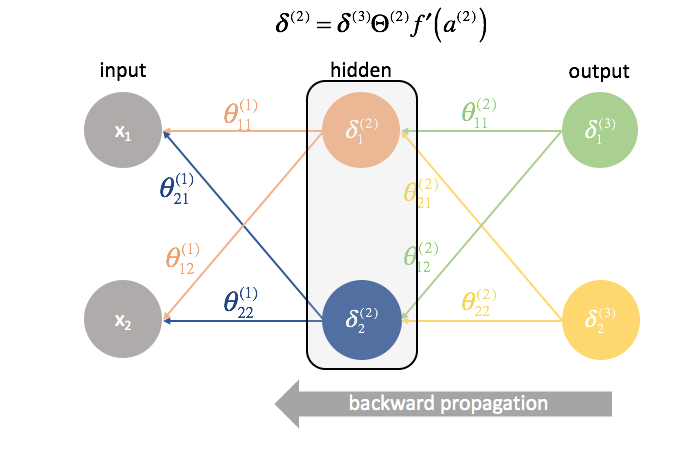

${{Theta ^{(1)}}$ è la matrice di parametri che collega lo strato 1 al 2. Moltiplichiamo l’errore dal secondo strato per gli ingressi nel primo strato per calcolare le nostre derivate parziali per questo set di parametri.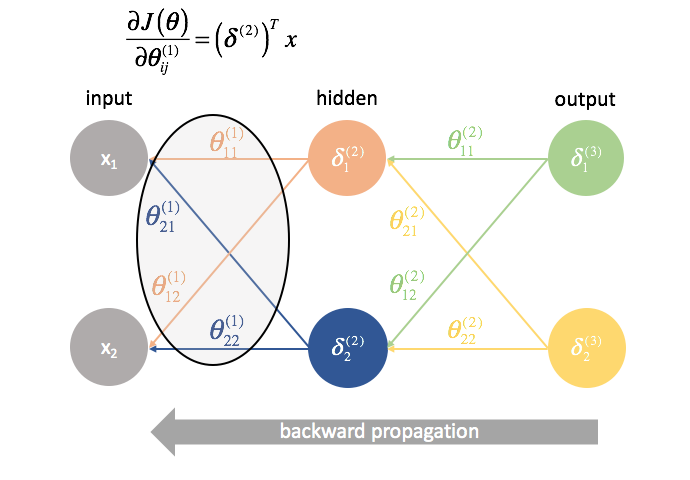

Per ogni strato eccetto l’ultimo, il termine “errore” è una combinazione lineare di parametri che si collegano allo strato successivo (avanzando attraverso la rete) e i termini “errore” dello strato successivo. Questo è vero per tutti gli strati nascosti, poiché non calcoliamo un termine di “errore” per gli ingressi.

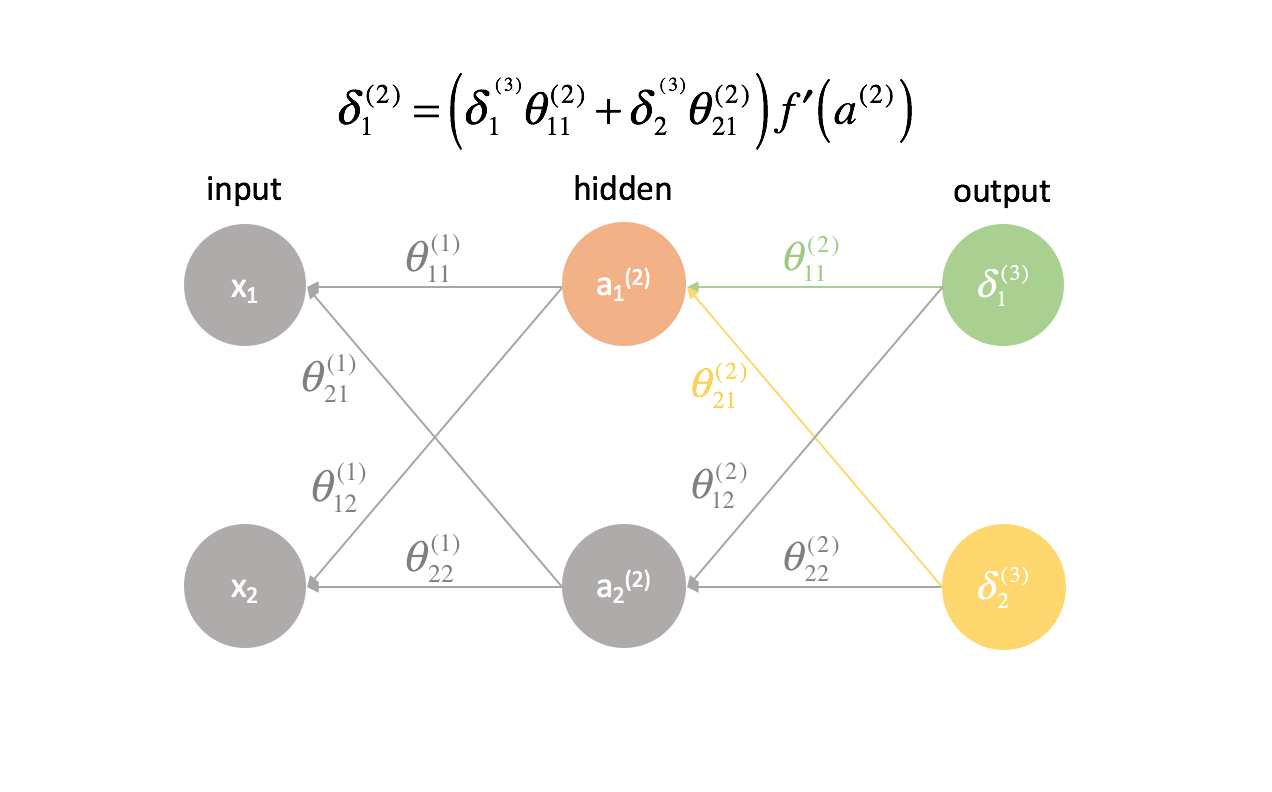
L’ultimo strato è un caso speciale perché calcoliamo i valori $\delta$ confrontando direttamente ogni neurone di uscita con il suo output atteso.

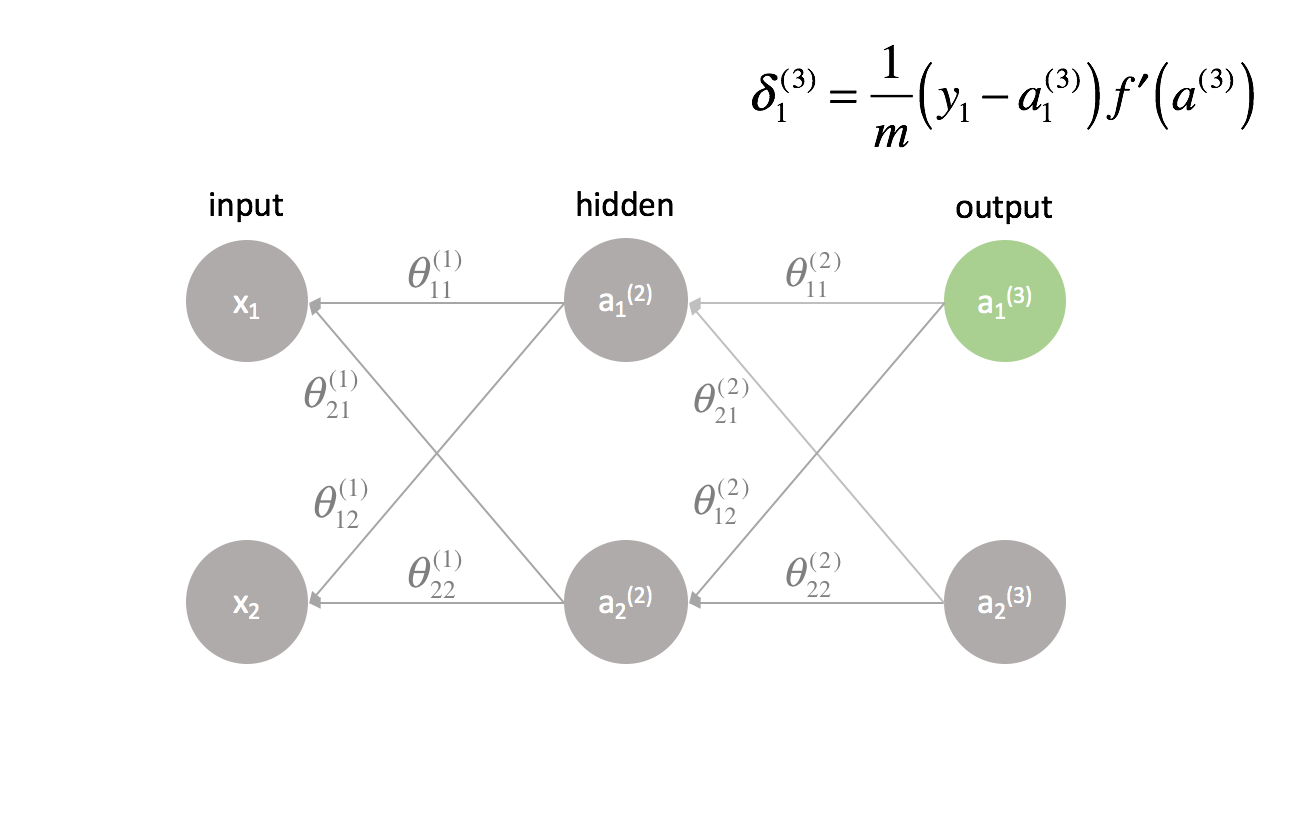
Un metodo formalizzato per implementare la backpropagation

Qui presenterò un metodo pratico per implementare la backpropagation attraverso una rete di strati $l=1,2,…,L$.

1. Eseguire la propagazione in avanti.

2. Computare il termine $delta$ per lo strato di uscita.

3. Computa le derivate parziali della funzione di costo rispetto a tutti i parametri che alimentano lo strato di uscita, ${{Theta ^{(L – 1)}}$.

4. Torna indietro di uno strato.
   $l = l – 1$

5. Computa il termine $\delta$ per lo strato nascosto corrente.

6. Computa le derivate parziali della funzione di costo rispetto a tutti i parametri che alimentano lo strato corrente.

7. Ripeti i punti da 4 a 6 fino a raggiungere lo strato di input.

Rivedere l’inizializzazione dei pesi

Quando abbiamo iniziato, ho proposto di inizializzare i nostri pesi in modo casuale per avere un punto di partenza. Questo ci ha permesso di eseguire la propagazione in avanti, confrontare le uscite con i valori attesi e calcolare il costo del nostro modello.

In realtà è molto importante inizializzare i nostri pesi a valori casuali in modo da poter rompere la simmetria nel nostro modello. Se avessimo inizializzato tutti i nostri pesi allo stesso modo, ogni neurone nello strato successivo sarebbe uguale alla stessa combinazione lineare di valori.

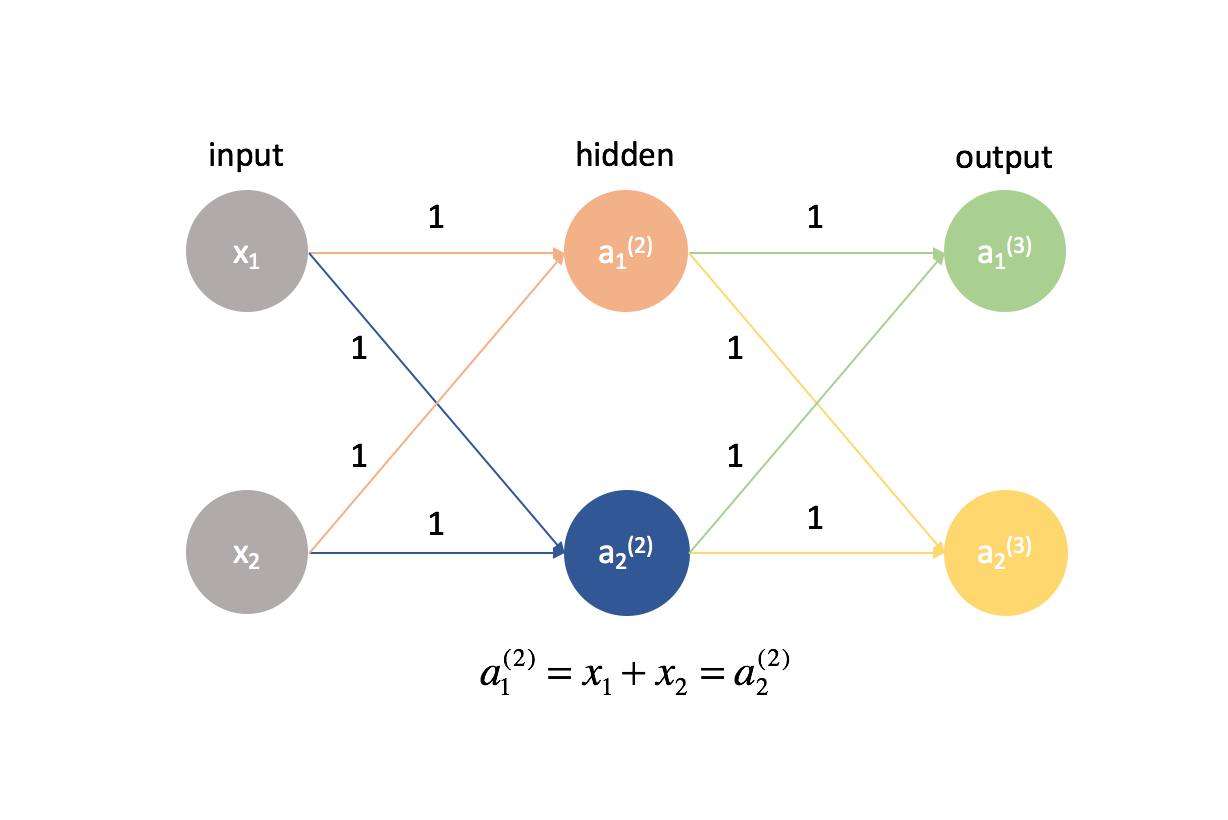
In base a questa stessa logica, anche i valori $\delta$ sarebbero gli stessi per ogni neurone in un dato strato.

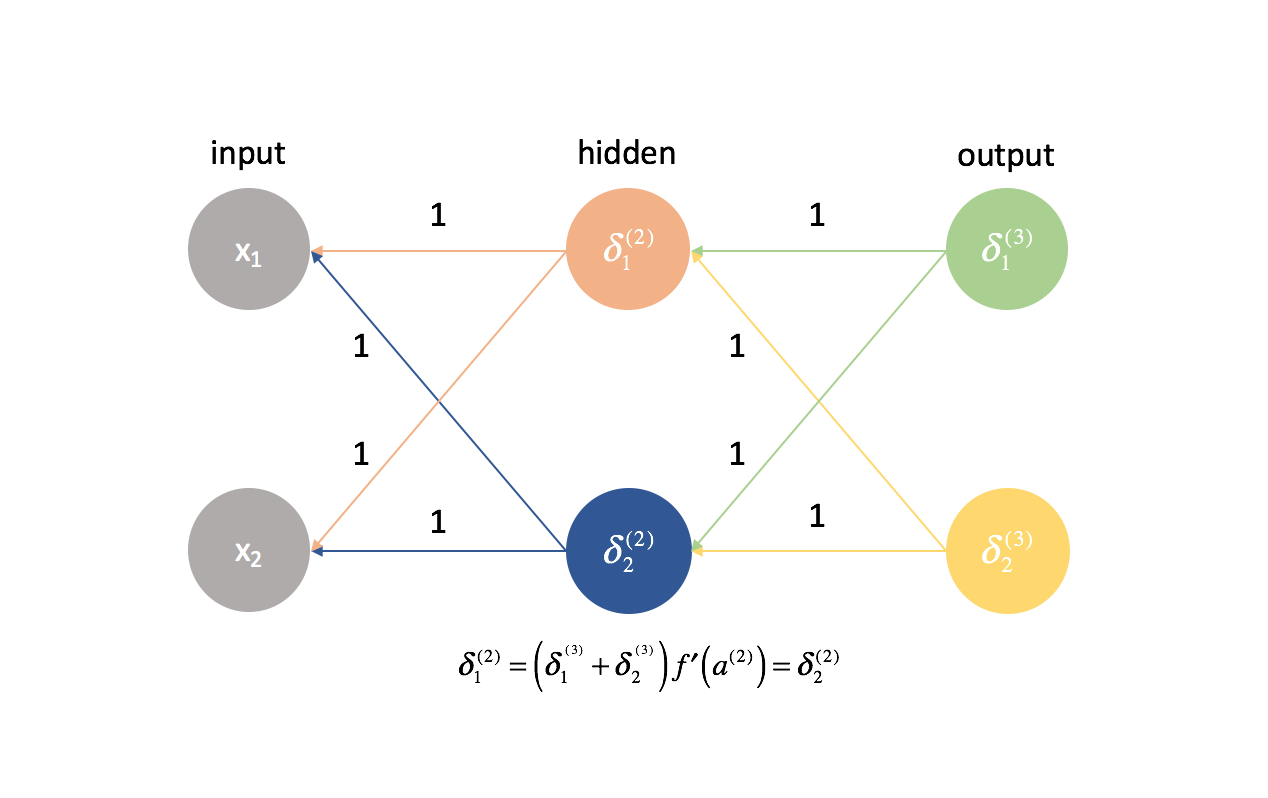
Inoltre, poiché calcoliamo le derivate parziali in ogni dato strato combinando i valori $delta$ e le attivazioni, tutte le derivate parziali in ogni dato strato sarebbero identiche. Come tale, i pesi si aggiornerebbero simmetricamente nella discesa del gradiente e più neuroni in ogni strato sarebbero inutili. Questa ovviamente non sarebbe una rete neurale molto utile.

Inizializzare casualmente i pesi della rete ci permette di rompere questa simmetria e aggiornare ogni peso individualmente secondo la sua relazione con la funzione di costo. Tipicamente assegneremo ad ogni parametro un valore casuale in $\left$ dove $\varepsilon$ è un valore vicino allo zero.

Mettere tutto insieme

Dopo aver calcolato tutte le derivate parziali dei parametri della rete neurale, possiamo usare la discesa a gradiente per aggiornare i pesi.

In generale, abbiamo definito la discesa a gradiente come

dove $\Delta {\theta _i}$ è il “passo” che facciamo camminando lungo il gradiente, scalato da un tasso di apprendimento, $\eta$.

Useremo questa formula per aggiornare ciascuno dei pesi, ricomputare la propagazione in avanti con i nuovi pesi, retropropagare l’errore, e calcolare il prossimo aggiornamento dei pesi. Questo processo continua fino a quando non convergiamo su un valore ottimale per i nostri parametri.

Durante ogni iterazione eseguiamo la propagazione in avanti per calcolare gli output e la propagazione all’indietro per calcolare gli errori; un’iterazione completa è nota come epoca. E’ comune riportare le metriche di valutazione dopo ogni epoca in modo da poter osservare l’evoluzione della nostra rete neurale mentre si allena.

Altra lettura

• Il calcolo matriciale di cui hai bisogno per il Deep Learning

• Come funziona l’algoritmo di backpropagation

• Stanford cs231n: Backpropagation, Intuizioni

• CS231n Inverno 2016: Lezione 4: Backpropagation, Reti Neurali 1

• Lezioni sull’Apprendimento Profondo

• Si dovrebbe capire la backprop

• Building blocks delle reti neurali

• E nel caso tu abbia appena rinunciato alla backpropagation… Apprendimento profondo senza Backpropagation