Il metodo dei moltiplicatori di Lagrange è il cavallo di battaglia degli economisti per risolvere i problemi di ottimizzazione. La tecnica è un elemento centrale della teoria economica, ma sfortunatamente viene solitamente insegnata male.
La maggior parte dei libri di testo si concentra sulla meccanica delle formule, lasciando gli studenti disorientati sul perché funziona davvero, tanto per cominciare. In questo post, spiegherò un modo semplice per vedere perché i moltiplicatori di Lagrange fanno effettivamente quello che fanno – cioè, risolvono problemi di ottimizzazione vincolata attraverso l’uso di una funzione lagrangiana semi-misteriosa.
Qualche informazione di base
Prima di poter vedere perché il metodo funziona, devi sapere qualcosa sui gradienti. Per funzioni di una variabile c’è – di solito – una derivata prima. Per funzioni di n variabili, ci sono n derivate prime. Un gradiente è solo un vettore che raccoglie tutte le derivate parziali prime della funzione in un unico posto.
Ogni elemento del gradiente è una delle derivate parziali prime della funzione. Un modo semplice per pensare al gradiente è che se scegliamo un punto su una funzione, questo ci dà la “direzione” in cui la funzione sta andando. Se la nostra funzione è etichettata
la notazione per il gradiente di f è
La cosa più importante da sapere sui gradienti è che puntano sempre nella direzione della pendenza più ripida di una funzione in un dato punto. Per aiutare ad illustrare questo, date un’occhiata al disegno qui sotto. Illustra come funzionano i gradienti per una funzione a due variabili di x1 e x2.
La funzione f nel disegno forma una collina. Verso il picco ho disegnato due regioni dove teniamo l’altezza di f costante ad un certo livello a. Queste sono chiamate curve di livello di f, e sono segnate f = a1, e f = a2.
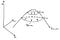
Immaginatevi in piedi su una di queste curve piane. Pensate a un sentiero escursionistico sul fianco di una montagna. In piedi sul sentiero, in quale direzione la montagna è più ripida? Chiaramente la direzione più ripida è quella dritta sulla collina, perpendicolare al sentiero. Nel disegno, questi percorsi di salita più ripida sono contrassegnati da frecce. Queste sono le pendenze
in vari punti lungo le curve di livello. Proprio come l’escursione più ripida è sempre perpendicolare al nostro sentiero, le pendenze di f sono sempre perpendicolari alle sue curve di livello.
Questa è l’idea chiave qui: le curve di livello sono dove
e
Come funziona il metodo
Per vedere come funzionano i moltiplicatori di Lagrange, date un’occhiata al disegno qui sotto. Ho ridisegnato la funzione f da sopra, insieme a un vincolo g = c. Nel disegno, il vincolo è un piano che taglia la nostra collina. Ho anche disegnato un paio di curve di livello di f.

Il nostro obiettivo qui è salire più in alto possibile sulla collina, dato che non possiamo muoverci più in alto di dove il vincolo g = c taglia la collina.
Nel disegno, il confine dove il vincolo taglia la funzione è segnato con una linea pesante. Lungo quella linea ci sono i punti più alti che possiamo raggiungere senza scavalcare il nostro vincolo. Questo è un posto ovvio per iniziare a cercare un massimo vincolato.
Immaginate di camminare da sinistra a destra sulla linea di vincolo. Man mano che guadagniamo quota, camminiamo attraverso varie curve di livello di f. Ne ho segnate due nell’immagine. Ad ogni curva di livello, immaginate di controllare la sua pendenza – cioè la pendenza di una linea tangente ad essa – e di confrontarla con la pendenza sul vincolo dove ci troviamo.
Se la nostra pendenza è maggiore della curva di livello, possiamo raggiungere un punto più alto della collina se continuiamo a muoverci verso destra. Se la nostra pendenza è minore della curva di livello – diciamo, verso destra dove la nostra linea di vincolo sta diminuendo – dobbiamo spostarci indietro a sinistra per raggiungere un punto più alto.
Quando raggiungiamo un punto in cui la pendenza della linea di vincolo è uguale alla pendenza della curva di livello, ci siamo spostati più in alto possibile. Cioè, abbiamo raggiunto il nostro massimo vincolato. Qualsiasi movimento da quel punto ci porterà in discesa. Nella figura, questo punto è segnato da una grande freccia che punta verso il picco.
In quel punto, la curva di livello f = a2 e il vincolo hanno la stessa pendenza. Questo significa che sono parallele e puntano nella stessa direzione. Ma come abbiamo visto sopra, le pendenze sono sempre perpendicolari alle curve di livello. Quindi se queste due curve sono parallele, anche i loro gradienti devono essere paralleli.
Questo significa che i gradienti di f e g puntano entrambi nella stessa direzione, e differiscono al massimo di uno scalare. Chiamiamo questo scalare “lambda”. Allora abbiamo,
Solvendo per zero, otteniamo
Questa è la condizione che deve tenere quando abbiamo raggiunto il massimo di f soggetto al vincolo g = c. Ora, se siamo intelligenti possiamo scrivere una singola equazione che catturi questa idea. È qui che entra in gioco la familiare equazione lagrangiana:
o più esplicitamente,
Per vedere come funziona questa equazione, guardate cosa succede quando seguiamo la solita procedura lagrangiana. Per prima cosa, troviamo le tre derivate parziali prime di L,
e impostarli uguali a zero. Cioè, dobbiamo impostare il gradiente di L uguale a zero. Per trovare il gradiente di L, prendiamo le tre derivate parziali di L rispetto a x1, x2 e lambda. Poi mettiamo ciascuna come elemento di un vettore 3 x 1. Questo ci dà quanto segue:
Ricordiamo che abbiamo due “regole” da seguire qui. Primo, i gradienti di f e g devono puntare nella stessa direzione, o
E secondo, dobbiamo soddisfare il nostro vincolo, oppure
Il primo e il secondo elemento del gradiente di L assicurano che la prima regola sia seguita. Cioè, costringono
assicurando che i gradienti di f e g puntino entrambi nella stessa direzione. Il terzo elemento del gradiente di L è semplicemente un trucco per assicurarsi che g = c, che è il nostro vincolo. Nella funzione lagrangiana, quando prendiamo la derivata parziale rispetto a lambda, ci restituisce semplicemente la nostra equazione di vincolo originale.
A questo punto, abbiamo tre equazioni in tre incognite. Quindi possiamo risolvere questo per i valori ottimali di x1 e x2 che massimizzano f soggetto al nostro vincolo. E abbiamo finito.
Così la linea di fondo è che i moltiplicatori di Lagrange è davvero solo un algoritmo che trova dove il gradiente di una funzione punta nella stessa direzione dei gradienti dei suoi vincoli, mentre soddisfa anche quei vincoli.
Come nella maggior parte delle aree della matematica, una volta che si vede il fondo delle cose – in questo caso, che l’ottimizzazione è davvero solo hill-climbing, che tutti capiscono – le cose sono molto più semplici di quanto molti economisti le fanno sembrare.