Dans mon premier post sur les réseaux neuronaux, j’ai discuté d’une représentation modèle pour les réseaux neuronaux et de la façon dont nous pouvons alimenter des entrées et calculer une sortie. Nous avons calculé cette sortie, couche par couche, en combinant les entrées de la couche précédente avec les poids pour chaque connexion neurone-neurone. J’ai mentionné que nous parlerions de la façon de trouver les poids appropriés pour connecter les neurones ensemble dans un prochain post – c’est ce post !
Overview
Dans le post précédent, j’avais juste supposé que nous avions une connaissance préalable magique des poids appropriés pour chaque réseau neuronal. Dans ce post, nous allons réellement comprendre comment faire en sorte que notre réseau neuronal « apprenne » les poids appropriés. Toutefois, pour avoir un point de départ, nous allons simplement initialiser chacun des poids avec des valeurs aléatoires à titre d’estimation initiale. Nous reviendrons sur cette étape d’initialisation aléatoire plus tard dans le post.
Au vu de nos poids initialisés de manière aléatoire reliant chacun des neurones, nous pouvons maintenant alimenter notre matrice d’observations et calculer les sorties de notre réseau neuronal. C’est ce qu’on appelle la propagation vers l’avant. Étant donné que nous avons choisi nos poids au hasard, notre sortie ne sera probablement pas très bonne par rapport à notre sortie attendue pour l’ensemble de données.
Alors, que faisons-nous à partir de là ?
Eh bien, pour commencer, définissons ce à quoi ressemble une » bonne » sortie. À savoir, nous allons développer une fonction de coût qui pénalise les sorties éloignées de la valeur attendue.
Puis, nous devons trouver un moyen de modifier les poids pour que la fonction de coût s’améliore. Tout chemin donné d’un neurone d’entrée à un neurone de sortie n’est essentiellement qu’une composition de fonctions ; en tant que tel, nous pouvons utiliser les dérivées partielles et la règle de la chaîne pour définir la relation entre tout poids donné et la fonction de coût. Nous pouvons utiliser cette connaissance pour ensuite tirer parti de la descente de gradient dans la mise à jour de chacun des poids.
Préalables
Lorsque j’ai commencé à apprendre la rétropropagation, de nombreuses personnes ont essayé d’abstraire les mathématiques sous-jacentes (chaînes dérivées) et je n’ai jamais vraiment pu saisir ce que diable se passait jusqu’à ce que je regarde la conférence du professeur Winston au MIT. J’espère que ce post donne une meilleure compréhension de la rétropropagation que simplement « c’est l’étape où nous envoyons l’erreur en arrière pour mettre à jour les poids ».
Pour bien saisir les concepts discutés dans ce post, vous devez être familier avec les éléments suivants :
Dérivées partielles
Ce post va être un peu dense avec beaucoup de dérivées partielles. Cependant, j’espère que même un lecteur sans connaissance préalable du calcul multivarié pourra suivre la logique derrière la rétropropagation.
Si vous n’êtes pas familier avec le calcul, $\frac{{\partial f\left( x \right)}}{{\partial x}}$ vous semblera probablement assez étranger. Vous pouvez interpréter cette expression comme « comment $f\left( x \right)$ change-t-il lorsque je modifie $x$ ? ». Cela sera utile car nous pourrons poser des questions telles que « Comment la fonction de coût change-t-elle lorsque je modifie ce paramètre ? Est-ce que cela augmente ou diminue la fonction de coût ? » pour rechercher les paramètres optimaux.
Si vous souhaitez vous remettre à niveau en calcul multivarié, consultez les leçons de Khan Academy sur le sujet.
Descente par gradient
Pour éviter que ce post ne devienne trop long, j’ai séparé le sujet de la descente par gradient dans un autre post. Si vous n’êtes pas familier avec cette méthode, assurez-vous de la lire ici et de la comprendre avant de poursuivre ce post.
Multiplication matricielle
Voici un rafraîchissement rapide de Khan Academy.
Démarrer simplement
Pour comprendre comment utiliser la descente de gradient dans la formation d’un réseau neuronal, commençons par le réseau neuronal le plus simple : un neurone d’entrée, un neurone de couche cachée et un neurone de sortie.

Pour montrer une image plus complète de ce qui se passe, j’ai développé chaque neurone pour montrer 1) la combinaison linéaire des entrées et des poids et 2) l’activation de cette combinaison linéaire. Il est facile de voir que l’étape de propagation vers l’avant est simplement une série de fonctions où la sortie de l’une alimente comme entrée de la suivante.
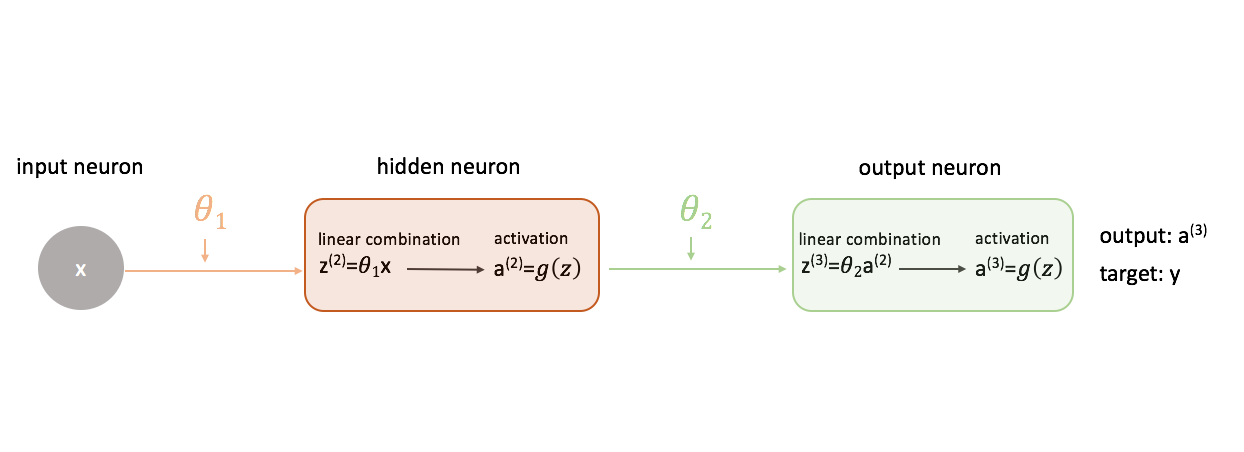
Définir une » bonne » performance dans un réseau neuronal
Définissons notre fonction de coût pour qu’elle soit simplement l’erreur au carré.
Il existe une myriade de fonctions de coût que nous pourrions utiliser, mais pour ce réseau neuronal, l’erreur au carré fonctionnera très bien.
Souvenez-vous que nous voulons évaluer la sortie de notre modèle par rapport à la sortie cible pour tenter de minimiser la différence entre les deux.
Relation des poids à la fonction de coût
Pour minimiser la différence entre la sortie de notre réseau neuronal et la sortie cible, nous devons savoir comment la performance du modèle change par rapport à chaque paramètre de notre modèle. En d’autres termes, nous devons définir la relation (lire : dérivée partielle) entre notre fonction de coût et chaque poids. Nous pouvons ensuite mettre à jour ces poids dans un processus itératif utilisant la descente de gradient.
Regardons d’abord $\frac{{{partiel J\left( \theta \right)}}{{partiel {\theta _2}}$. Gardez la figure suivante à l’esprit pendant que nous progressons.
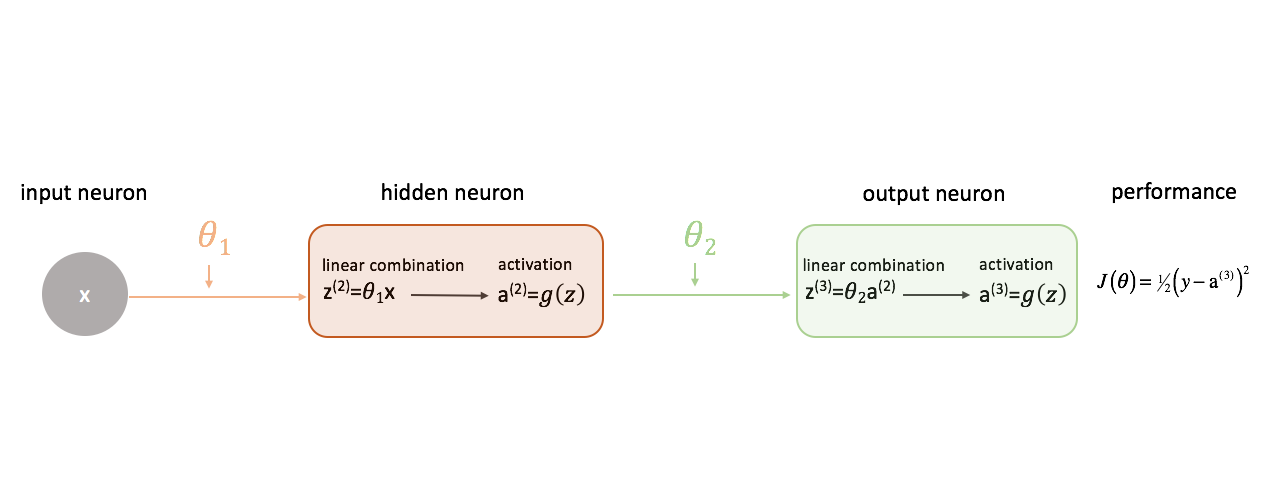
Prenons un moment pour examiner comment nous pourrions exprimer la relation entre $J\left( \theta \right)$ et $\theta _2$. Notez comment $\theta _2$ est une entrée de ${z^{(3)}}$, qui est une entrée de ${\rm{a}}^{(3)}}$, qui est une entrée de $J\left( \theta \right)$. Lorsque nous essayons de calculer une dérivée de ce genre, nous pouvons utiliser la règle de la chaîne pour résoudre.
Pour rappel, la règle de la chaîne énonce :
Appliquons la règle de la chaîne pour résoudre ${frac{{{partiel J\left( \theta \right)}}{{\partiel {\theta _2}}$.
Par une logique similaire, nous pouvons trouver $\frac{{partial J\left( \theta \right)}}{\partial {\theta _1}}$.
Pour plus de clarté, j’ai mis à jour notre diagramme de réseau neuronal pour visualiser ces chaînes. Assurez-vous d’être à l’aise avec ce processus avant de poursuivre.
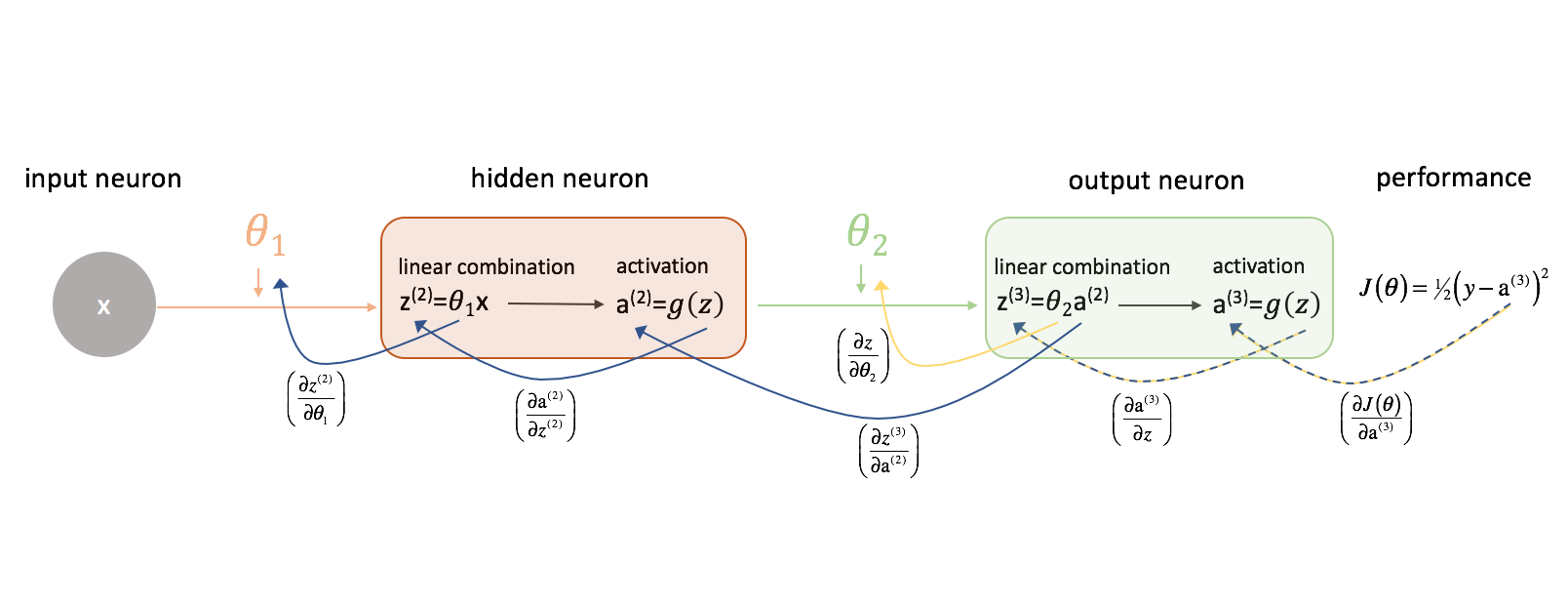
Ajouter de la complexité
Essayons maintenant cette même approche sur un exemple légèrement plus compliqué. Maintenant, nous allons examiner un réseau neuronal avec deux neurones dans notre couche d’entrée, deux neurones dans une couche cachée et deux neurones dans notre couche de sortie. Pour l’instant, nous ne tiendrons pas compte des neurones de biais qui manquent dans les couches d’entrée et cachées.
Prenons une seconde pour revoir la notation que je vais utiliser afin que vous puissiez suivre ces diagrammes. L’exposant (1) indique la couche dans laquelle se trouve l’objet et l’indice indique le neurone auquel nous nous référons dans une couche donnée. Par exemple, $a_1^{(2)}$ est l’activation du premier neurone de la deuxième couche. Pour les valeurs de paramètre ${\theta$, j’aime les lire comme une étiquette de courrier – la première valeur indique à quel neurone l’entrée est envoyée dans la couche suivante, et la deuxième valeur indique de quel neurone l’information est envoyée. Par exemple, ${\theta _{21}^{(2)}}$ est utilisé pour envoyer une entrée au 2ème neurone, à partir du 1er neurone de la couche 2. L’exposant désignant la couche correspond à l’endroit d’où provient l’entrée. Cette notation est cohérente avec la représentation matricielle dont nous avons parlé dans mon post sur la représentation des réseaux de neurones.
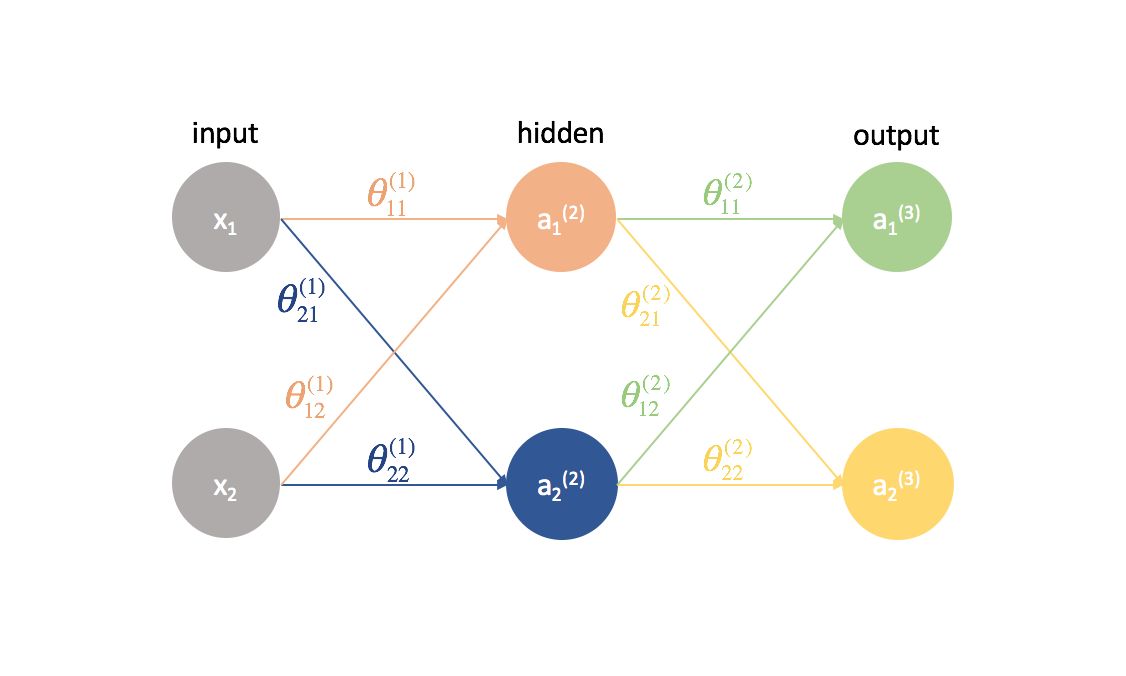
Détaillons ce réseau pour exposer toutes les mathématiques qui s’y déroulent.
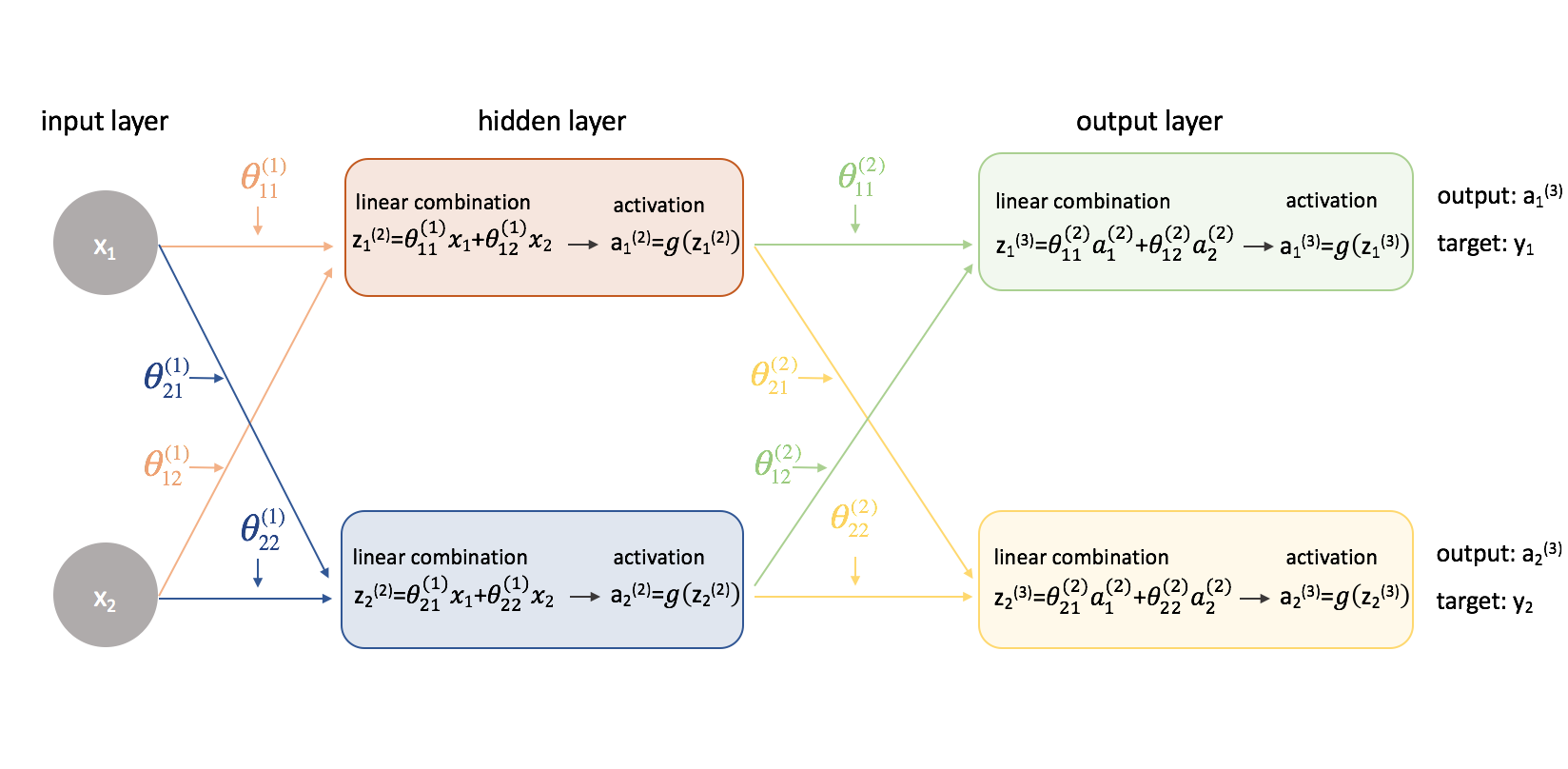
Ok ! Les choses se sont un peu plus compliquées. Je vais parcourir le processus pour trouver l’une des dérivées partielles de la fonction de coût par rapport à l’une des valeurs des paramètres ; je laisserai le reste des calculs comme un exercice pour le lecteur (et posterai les résultats finaux ci-dessous).
En premier lieu, nous devrons revoir notre fonction de coût maintenant que nous avons affaire à un réseau neuronal avec plus d’une sortie. Utilisons maintenant l’erreur quadratique moyenne comme notre fonction de coût.
Note : Si vous vous entraînez sur plusieurs observations (ce qui sera toujours le cas en pratique), nous devrons également effectuer une sommation de la fonction de coût sur tous les exemples d’entraînement. Pour cette fonction de coût, il est courant de normaliser par $\frac{1}{m}}$ où $m$ est le nombre d’exemples dans votre ensemble de données de formation.
Maintenant que nous avons corrigé notre fonction de coût, nous pouvons regarder comment le changement d’un paramètre affecte la fonction de coût. Plus précisément, je vais calculer $\frac{{\partial J\left( \theta \right)}}{\partial \theta _{11}^{(1)}}$ dans cet exemple. En regardant le diagramme, $\theta _{11}^{(1)}$ affecte la sortie à la fois pour $a _1^{(3)}$ et $a _2^{(3)}$. Comme notre fonction de coût est une somme de coûts individuels pour chaque sortie, nous pouvons calculer la chaîne dérivée pour chaque chemin et simplement les additionner.
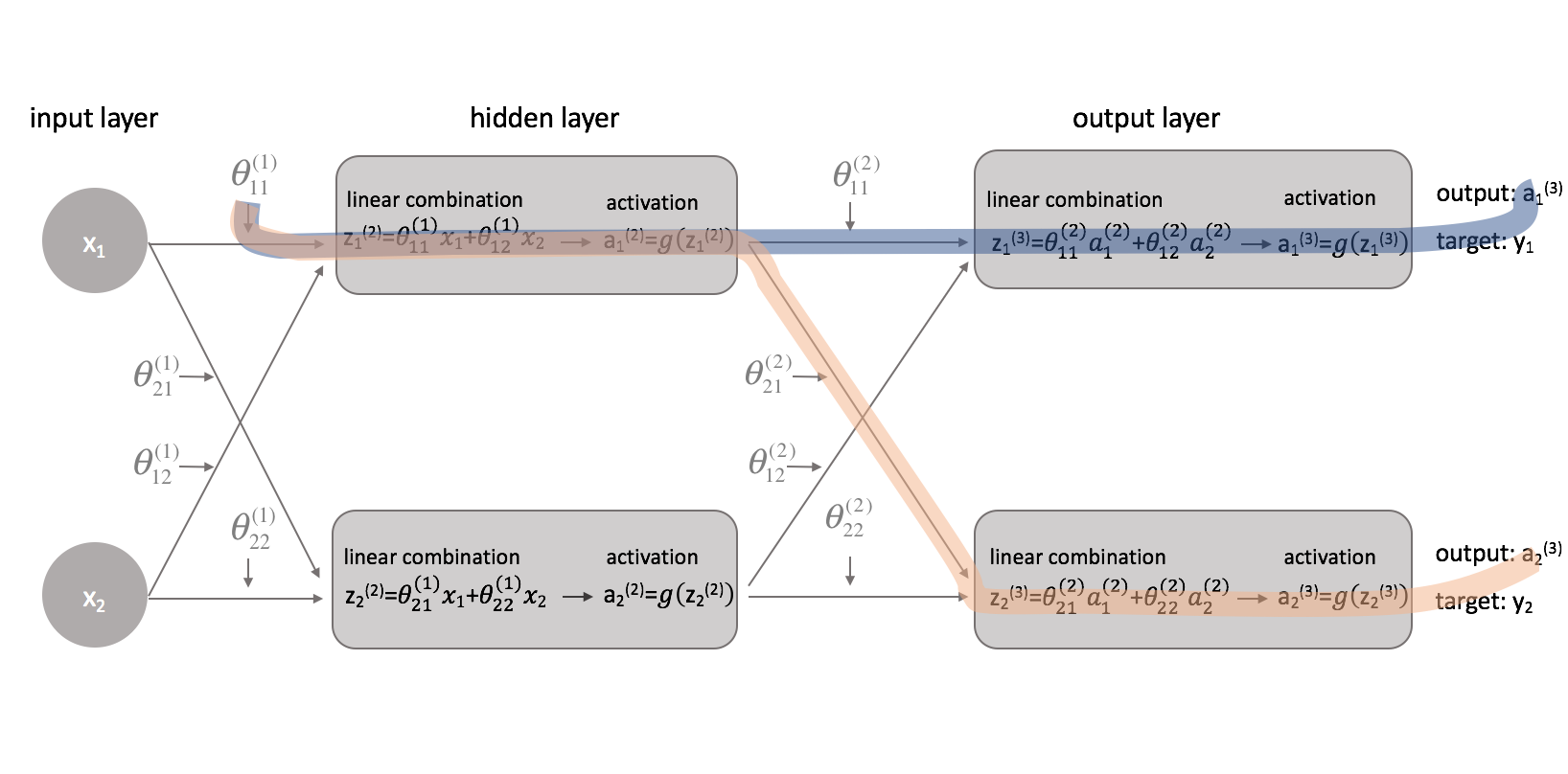
La chaîne dérivée pour le chemin bleu est:
$ \left( {\frac{{\partial J\left( \theta \right)}}{{\partial {\rm{a}}. _1^{(3)}}}} \right)\left( {\frac{\partial {\rm{a}} _1^{(3)}}{{partiel z _1^{(3)}}}} \right)\left( {\frac{\partial z _1^{(3)}}{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\c}{partial {\rm{a}} _1^{(2)}}{{partiel z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)}}}} \right) $
La chaîne de dérivée du chemin orange est:
$ \left( {\frac{{\partial J\left( \theta \right)}}{\partial \rm{a}} _2^{(3)}}}} \right)\left( {\frac{\partial {\rm{a}} _2^{(3)}}{{partiel z _2^{(3)}}}} \right)\left( {\frac{{\partial z _2^{(3)}}}{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{\partial {\rm{a}} _1^{(2)}}{{partiel z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)}}}} \right)$
En les combinant, nous obtenons l’expression totale de $\frac{{{partial J\left( \theta \right)}}{{partial \theta _{11}^{(1)}}$.
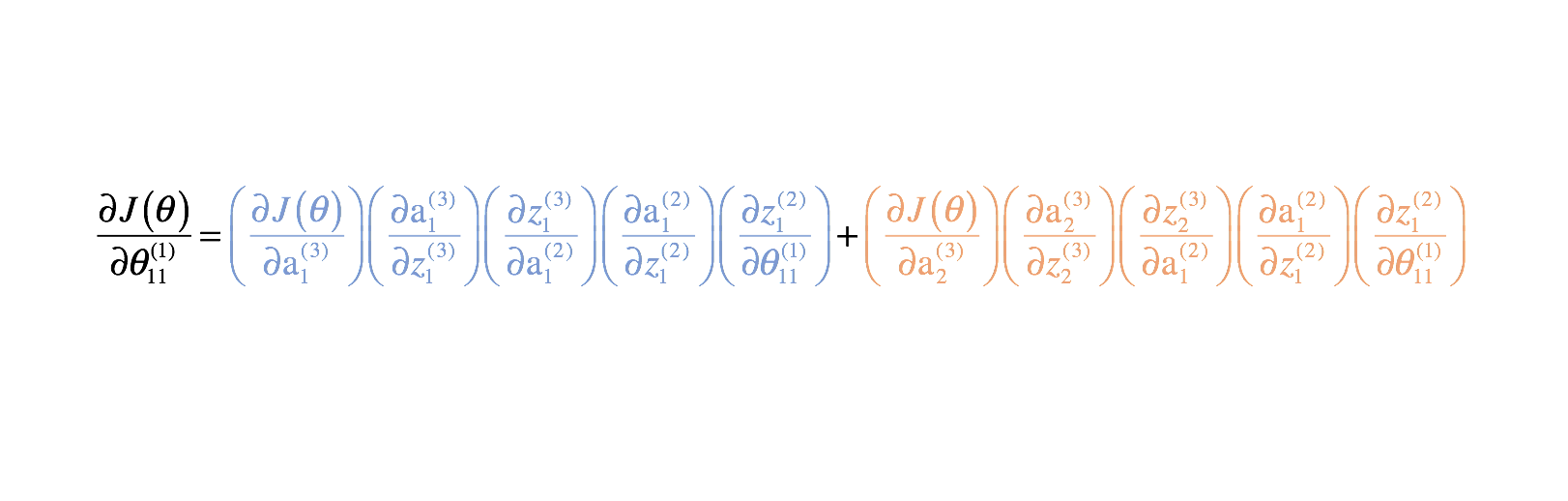
J’ai fourni le reste des dérivées partielles ci-dessous. Rappelez-vous, nous avons besoin de ces dérivées partielles car elles décrivent comment la modification de chaque paramètre affecte la fonction de coût. Ainsi, nous pouvons utiliser ces connaissances pour modifier toutes les valeurs des paramètres de manière à continuer à diminuer la fonction de coût jusqu’à ce que nous convergions vers une certaine valeur minimale.
Paramètres de la couche 2
Paramètres de la couche 1
Woah là. Nous venons de passer d’un réseau neuronal à 2 paramètres nécessitant 8 termes de dérivée partielle dans l’exemple précédent à un réseau neuronal à 8 paramètres nécessitant 52 termes de dérivée partielle. Cela va rapidement devenir incontrôlable, surtout si l’on considère que de nombreux réseaux neuronaux utilisés dans la pratique sont beaucoup plus grands que ces exemples.
Heureusement, en regardant de plus près, beaucoup de ces dérivées partielles sont répétées. Si nous sommes intelligents sur la façon dont nous abordons ce problème, nous pouvons réduire considérablement le coût computationnel de la formation. En outre, il serait vraiment pénible de devoir calculer manuellement les chaînes de dérivées pour chaque paramètre. Regardons ce que nous avons fait jusqu’à présent et voyons si nous pouvons généraliser une méthode à cette folie.
Généraliser une méthode
Examinons les dérivées partielles ci-dessus et faisons quelques observations. Nous allons commencer par examiner les dérivées partielles par rapport aux paramètres de la couche 2. Rappelez-vous, les paramètres dans pour la couche 2 sont combinés avec les activations de la couche 2 pour alimenter comme entrées la couche 3.
Paramètres de la couche 2
Analysons les expressions suivantes ; je vous encourage à résoudre les dérivées partielles au fur et à mesure pour vous convaincre de ma logique.
En premier lieu, il semble que les colonnes contiennent des valeurs très similaires. Par exemple, la première colonne contient les dérivées partielles de la fonction de coût par rapport aux sorties du réseau neuronal. En pratique, il s’agit de la différence entre la sortie attendue et la sortie réelle (puis mise à l’échelle par $m$) pour chacun des neurones de sortie.
La deuxième colonne représente la dérivée de la fonction d’activation utilisée dans la couche de sortie. Notez que pour chaque couche, les neurones utiliseront la même fonction d’activation. Une fonction d’activation homogène au sein d’une couche est nécessaire pour pouvoir tirer parti des opérations matricielles dans le calcul de la sortie du réseau neuronal. Ainsi, la valeur de la deuxième colonne sera la même pour les quatre termes.
La première et la deuxième colonnes peuvent être combinées sous la forme de $\delta _i^{(3)}$ pour des raisons de commodité plus tard dans la route. Il n’est pas immédiatement évident de savoir pourquoi cela serait utile, mais vous verrez en remontant une autre couche pourquoi cela est utile. Les gens font souvent référence à cette expression comme le terme « erreur » que nous utilisons pour « renvoyer l’erreur de la sortie à travers le réseau ». Nous verrons bientôt pourquoi c’est le cas. Chaque neurone du réseau aura un terme $\delta$ correspondant que nous allons résoudre.
La troisième colonne représente la façon dont le paramètre d’intérêt change par rapport aux entrées pondérées pour la couche actuelle ; lorsque vous calculez la dérivée, cela correspond à l’activation de la couche précédente.
J’aimerais également noter que les deux premiers termes de la dérivée partielle semblent concernés par le premier neurone de sortie (neurone 1 de la couche 3) tandis que les deux derniers termes de la dérivée partielle semblent concernés par le deuxième neurone de sortie (neurone 2 de la couche 3). Ceci est évident dans le terme $\frac{{{partial J\left( \theta \right)}}{{\partial {\rm{a}}_i^{(3)}}$. Utilisons cette connaissance pour réécrire les dérivées partielles en utilisant l’expression $\delta$ que nous avons définie plus haut.
$ \frac{{\partial J\left( \theta \right)}}{\partial \theta _{12}^{(2)}} = \delta _1^{(3)}\left( {\frac{\partial z _1^{(3)}}{\partial \theta _{12}^{(2)}}}} \right) $
$ \frac{{{\partial J\left( \theta \right)}}{{\partial \theta _{21}^{(2)}} = \delta _2^{(3)}\left( {\frac{{\partial z _2^{(3)}}{{\partial \theta _{21}^{(2)}}}} \right) $
$ \frac{{{\partial J\left( \theta \right)}}{{\partial \theta _{22}^{(2)}} = \delta _2^{(3)}\left( {\frac{{\partial z _2^{(3)}}{{\partial \theta _{22}^{(2)}}}} \right) $
Après, allons-y et calculons le dernier terme de la dérivée partielle. Comme nous l’avons noté, cette dérivée partielle finit par représenter les activations de la couche précédente.
Note : je trouve utile d’utiliser le graphique du réseau neuronal étendu de la section précédente lors du calcul des dérivées partielles.
$ \frac{\partial J\left( \theta \right)}}{\partial \theta _{12}^{(2)}} = \delta _1^{(3)}{\rm{a}} _2^{(2)} $
$ \frac{{\i1}partiel J\left( \theta \right)}{\i1}partiel \theta _{21}^{(2)}} = \delta _2^{(3)}{\rm{a}} _1^{(2)} $
$ \frac{{\i1}partiel J\left( \theta \right)}{\i1}partiel \theta _{22}^{(2)}} = \delta _2^{(3)}{\rm{a}} _2^{(2)} $
Il semble que nous combinions les termes « erreur » avec les activations de la couche précédente pour calculer chaque dérivée partielle. Il est également intéressant de noter que les indices $j$ et $k$ pour $\theta _{jk}$ correspondent aux indices combinés de $\delta _j^{(3)}$ et ${\rm{a}}}. _k^{(2)}$.
Voyons si nous pouvons trouver une opération matricielle pour calculer toutes les dérivées partielles en une seule expression.
${\delta ^{(3)}}$ est un vecteur de longueur $j$ où $j$ est égal au nombre de neurones de sortie.
δ (3) = f ′ ( a (3) )
${\rm{a}}^{(2)}$ est un vecteur de longueur $k$ où $k$ est égal au nombre de neurones de la couche précédente. Les valeurs de ce vecteur représentent les activations de la couche précédente calculées pendant la propagation vers l’avant ; en d’autres termes, c’est le vecteur des entrées de la couche de sortie.
$ {a^{(2)}} = \left $
En multipliant ces vecteurs ensemble, nous pouvons calculer tous les termes de la dérivée partielle en une seule expression.
∂J( θ ) ∂ θ ij (2) ==
Pour résumer, voir le graphique ci-dessous.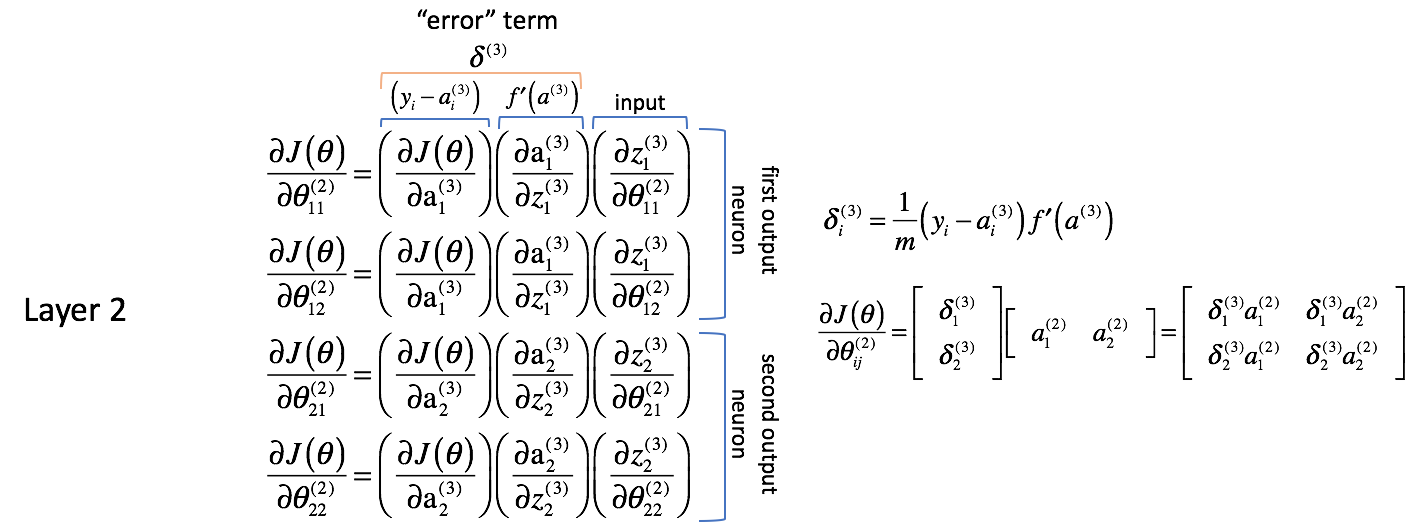
Note : techniquement, la première colonne devrait également être mise à l’échelle par $m$ pour être une dérivée exacte. Cependant, mon objectif était de souligner que c’est la colonne où nous sommes concernés par la différence entre les sorties attendues et réelles. Le terme $\delta$ à droite a l’expression complète de la dérivée.
Paramètres de la couche 1
Maintenant, jetons un coup d’œil et voyons ce qui se passe dans la couche 1.
Alors que les poids de la couche 2 n’affectaient directement qu’une sortie, les poids de la couche 1 affectent toutes les sorties. Rappelez-vous le graphique suivant.

Il en résulte qu’une dérivée partielle de la fonction de coût par rapport à un paramètre devient maintenant une somme de différentes chaînes. Plus précisément, nous aurons une chaîne de dérivée pour chaque $\delta$ que nous avons calculé dans la prochaine couche en avant. Rappelez-vous que nous avons commencé à la fin du réseau et que nous remontons le fil du réseau. Ainsi, la couche suivante vers l’avant représente les valeurs de $\delta$ que nous avons calculées précédemment.
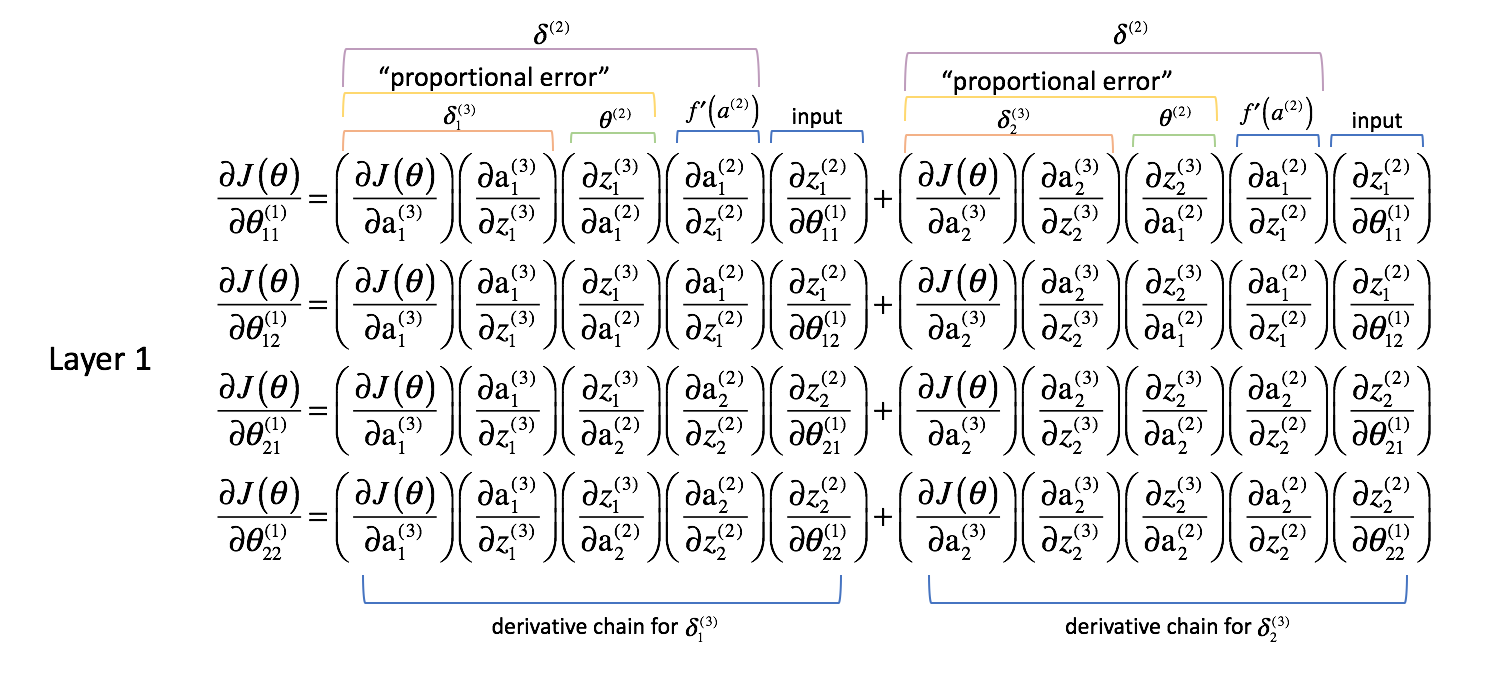
Comme nous l’avons fait pour la couche 2, faisons quelques observations.
Les deux premières colonnes (de chaque terme additionné) correspondent à un $\delta _j^{(3)}$ calculé dans la prochaine couche en avant (rappelez-vous, nous avons commencé à la fin du réseau et nous remontons).
La troisième colonne correspond à un certain paramètre qui relie la couche 2 à la couche 3. Si nous avons considéré $\delta _j^{(3)}$ comme un certain terme d' »erreur » pour la couche 3, et que chaque chaîne dérivée est maintenant une somme de ces erreurs, alors cette troisième colonne nous permet de pondérer chaque erreur respective. Ainsi, les trois premiers termes combinés représentent une certaine mesure de l’erreur proportionnelle.
Nous allons également redéfinir $\delta$ pour toutes les couches, à l’exception de la couche de sortie, afin d’inclure cette combinaison d’erreurs pondérées.
$ \delta _j^{(l)} = f’\left( {{a^{(l)}}) \right)\sum\limits _{i = 1}^n {\delta _i^{(l + 1)}\theta _{ij}^{(l)}}
Nous pourrions écrire ceci plus succinctement en utilisant des expressions matricielles.
$$ {\delta ^{(l)}} = {\delta ^{(l + 1)}{\Theta ^{(l)}}f’\left( {{a^{(l)}}} \droite) $
Note : Il est d’usage de désigner les vecteurs par des lettres minuscules et les matrices par des lettres majuscules. Ainsi, $\theta$ représente un vecteur tandis que $\Theta$ représente une matrice.
La quatrième colonne représente la dérivée de la fonction d’activation utilisée dans la couche courante. Rappelez-vous que pour chaque couche, les neurones utiliseront la même fonction d’activation.
Enfin, la cinquième colonne représente les différentes entrées de la couche précédente. Dans ce cas, il s’agit des entrées réelles du réseau neuronal.
Regardons de plus près l’un des termes, $\frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}}$.
En premier lieu, nous avons établi que les deux premières colonnes de chaque chaînes de dérivées ont été précédemment calculées comme $\delta _j^{(3)}$.
$ \frac{{\partial J\left( \theta \right)}}{\partial \theta _{11}^{(1)}} = \delta _1^{(3)}\left( {\frac{{\partial z _1^{(3)}}{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\c}{partial {\rm{a}} _1^{(2)}}{{partiel z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)}}}} \right) + \delta _2^{(3)}\left( {\frac{{\partial z _2^{(3)}}{{\partial {\rm{a}}} _1^{(2)}}}} \right)\left( {\frac{\partial {\rm{a}} _1^{(2)}}{{partiel z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)}}}} \right) $
De plus, nous avons établi que les troisièmes colonnes de chaque chaîne dérivée était un paramètre qui agissait pour pondérer chacun des termes $\delta$ respectifs. Nous avons également établi que la quatrième colonne était la dérivée de la fonction d’activation.
$ \frac{{\partial J\left( \theta \right)}{{\partial \theta _{11}^{(1)}} = \delta _1^{(3)}\theta _{11}^{(2)}f’\left( {{a^{(2)}}} \right)\left( {\frac{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)} }}}} \right) + \delta _2^{(3)}\theta _{21}^{(2)}f’\left( {{a^{(2)}} \right)\left( {\frac{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)} }}}} \right) $
Factoring out $\left( {\frac{{\partial z_1^{(2)}}{\partial \theta _{11}^{(1)}}}} \right)$,
$ \frac{{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \left( {\frac{{\partial z _1^{(2)}}{{\partial \theta _{11}^{(1)}}}} \right)\left( {\delta _1^{(3)}\theta _{11}^{(2)}f’\left( {{a^{(2)}}} \right) + \delta _2^{(3)}\theta _{21}^{(2)}f’\left( {{a^{(2)}}} \right)} \right) $
On se retrouve avec notre nouvelle définition de $\delta_j^{(l)}$. Allons-y et substituons-la.
$ \frac{{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \left( {\frac{{\partial z _1^{(2)}}{\partial \theta _{11}^{(1)}00} \right)\left( {\delta _1^{(2)}} \right) $
Enfin, nous avons établi que la cinquième colonne (${\frac{{\partial z_1^{(2)}}{\partial \theta_{11}^{(1)}}}}$) correspondait à une entrée de la couche précédente. Dans ce cas, la dérivée calculée est $x_1$.
$ \frac{{{partial J\left( \theta \right)}{{partial \theta _{11}^{(1)}} = \delta _1^{(2)}{x _1} $
Découvrons à nouveau une opération matricielle pour calculer toutes les dérivées partielles en une seule expression.
$\delta ^{(2)}$ est un vecteur de longueur $j$ où $j$ est le nombre de neurones dans la couche courante (couche 2). Nous pouvons calculer $\delta ^{(2)}$ comme la combinaison pondérée des erreurs de la couche 3, multipliée par la dérivée de la fonction d’activation utilisée dans la couche 2.
δ (2) = f ′ ( a (2) )=
$x$ est un vecteur de valeurs d’entrée.
En multipliant ces vecteurs ensemble, nous pouvons calculer tous les termes de la dérivée partielle en une seule expression.
∂J( θ ) ∂ θ ij (1) ==
Si vous êtes arrivé jusqu’ici, félicitations ! Nous venons de calculer toutes les dérivées partielles nécessaires pour utiliser la descente de gradient et optimiser les valeurs de nos paramètres. Dans la prochaine section, je présenterai un moyen de visualiser le processus que nous venons de développer, ainsi qu’une méthode complète pour mettre en œuvre la rétropropagation. Si vous comprenez tout jusqu’à ce point, cela devrait être une navigation sans heurts à partir de maintenant.
Backpropagation
Dans la dernière section, nous avons développé un moyen de calculer toutes les dérivées partielles nécessaires à la descente de gradient (dérivée partielle de la fonction de coût par rapport à tous les paramètres du modèle) en utilisant des expressions matricielles. Pour calculer les dérivées partielles, nous avons commencé à la fin du réseau et, couche par couche, nous sommes revenus au début. Nous avons également développé un nouveau terme, $\delta$, qui sert essentiellement à représenter tous les termes de dérivées partielles que nous aurions besoin de réutiliser plus tard et nous progressons, couche par couche, en arrière dans le réseau.
Note : La rétropropagation est simplement une méthode pour calculer la dérivée partielle de la fonction de coût par rapport à tous les paramètres. L’optimisation réelle des paramètres (formation) se fait par descente de gradient ou une autre technique d’optimisation plus avancée.
Généralement, nous avons établi que vous pouvez calculer les dérivées partielles pour la couche $l$ en combinant les termes $\delta$ de la couche suivante en avant avec les activations de la couche actuelle.
$ \frac{\partial J\left( \theta \right)}}{\partial \theta _{ij}^{(l)}} = {\left( {{\delta ^{(l + 1)}}} \right)^T}{a^{(l)}} $
La rétropropagation visualisée
Avant de définir la méthode formelle de la rétropropagation, j’aimerais proposer une visualisation du processus.
D’abord, nous devons calculer la sortie d’un réseau neuronal via la propagation en avant.
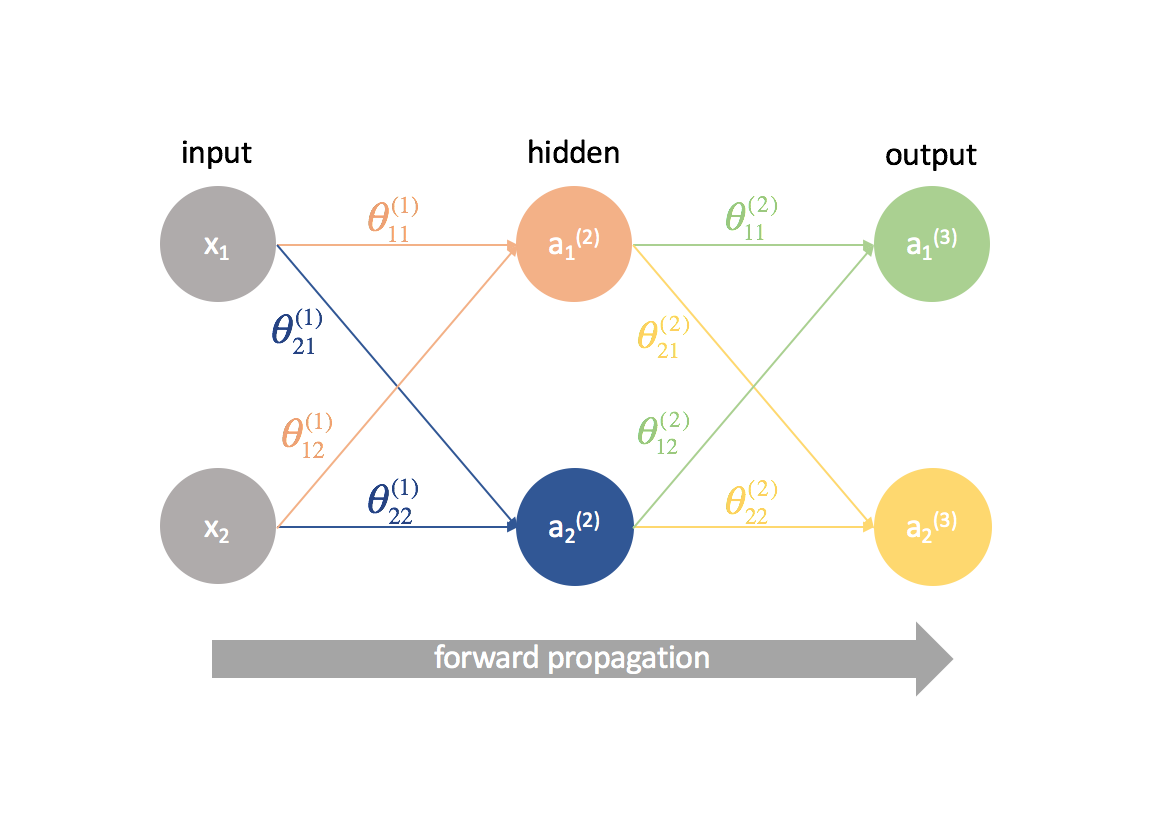
Puis, nous calculons les termes ${\delta ^{(3)}}$ pour la dernière couche du réseau. Rappelez-vous, ces termes ${delta$ sont constitués de toutes les dérivées partielles qui seront à nouveau utilisées pour calculer les paramètres des couches plus en arrière. En pratique, on appelle généralement $\delta$ le terme » erreur « .
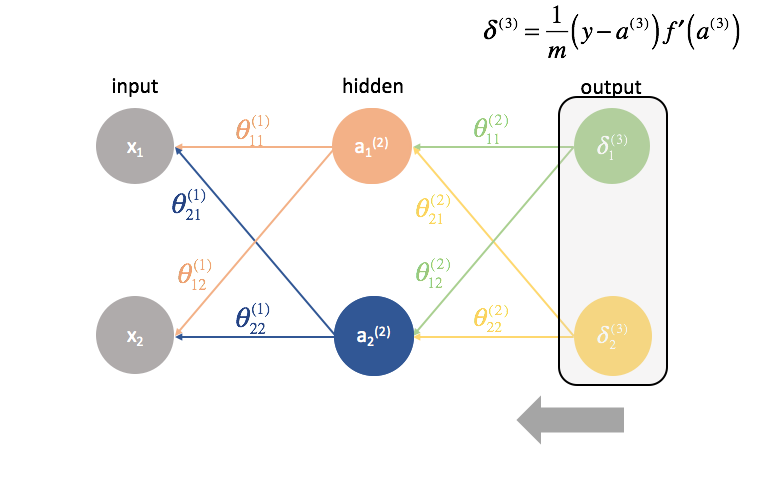
${\ta ^{(2)}}$ est la matrice des paramètres qui relie la couche 2 à la couche 3. Nous multiplions l’erreur de la troisième couche par les entrées de la deuxième couche pour calculer nos dérivées partielles pour cet ensemble de paramètres.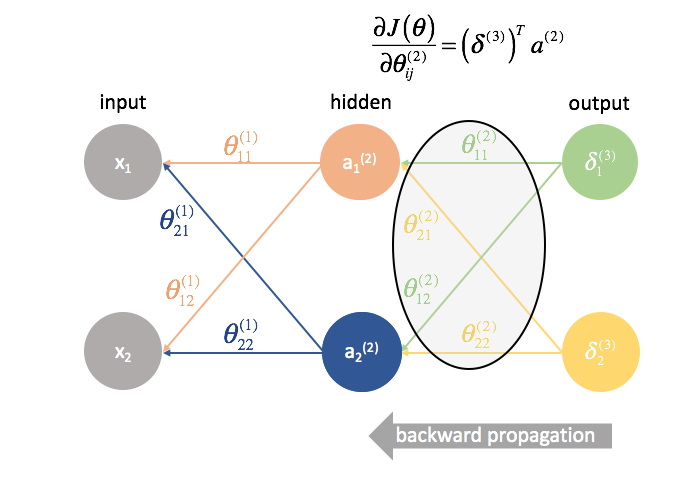
Puis, nous « renvoyons » les termes « erreur » exactement de la même manière que nous « envoyons » les entrées à un réseau neuronal. La seule différence est que cette fois, nous partons de l’arrière et nous alimentons un terme d’erreur, couche par couche, en arrière dans le réseau. D’où le nom : rétropropagation. L’acte de » renvoyer notre erreur » s’effectue via l’expression ${\delta ^{(3)}}{\Theta ^{(2)}}$.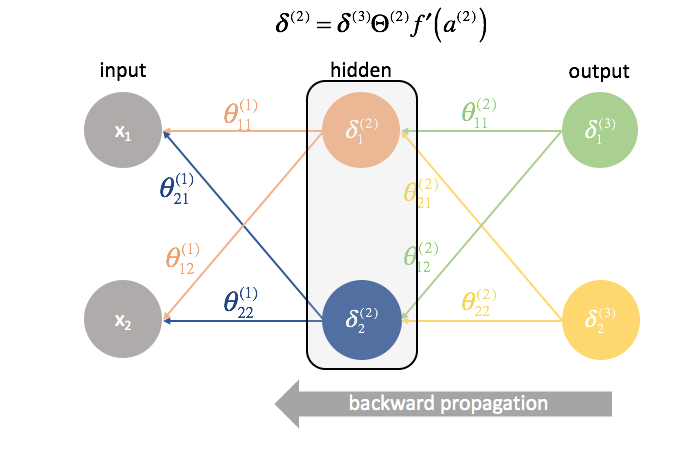
${\ta ^{(1)}}$ est la matrice de paramètres qui relie la couche 1 à la couche 2. Nous multiplions l’erreur de la deuxième couche par les entrées de la première couche pour calculer nos dérivées partielles pour cet ensemble de paramètres.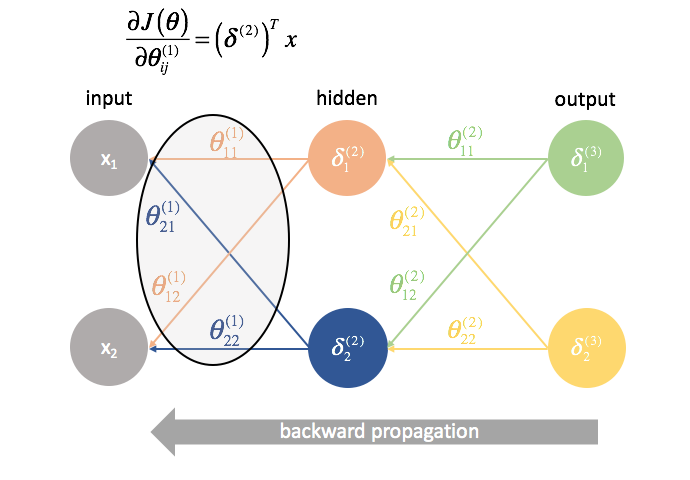
Pour chaque couche, à l’exception de la dernière, le terme « erreur » est une combinaison linéaire de paramètres se connectant à la couche suivante (en avançant dans le réseau) et des termes « erreur » de cette couche suivante. Ceci est vrai pour toutes les couches cachées, puisque nous ne calculons pas de terme « erreur » pour les entrées.
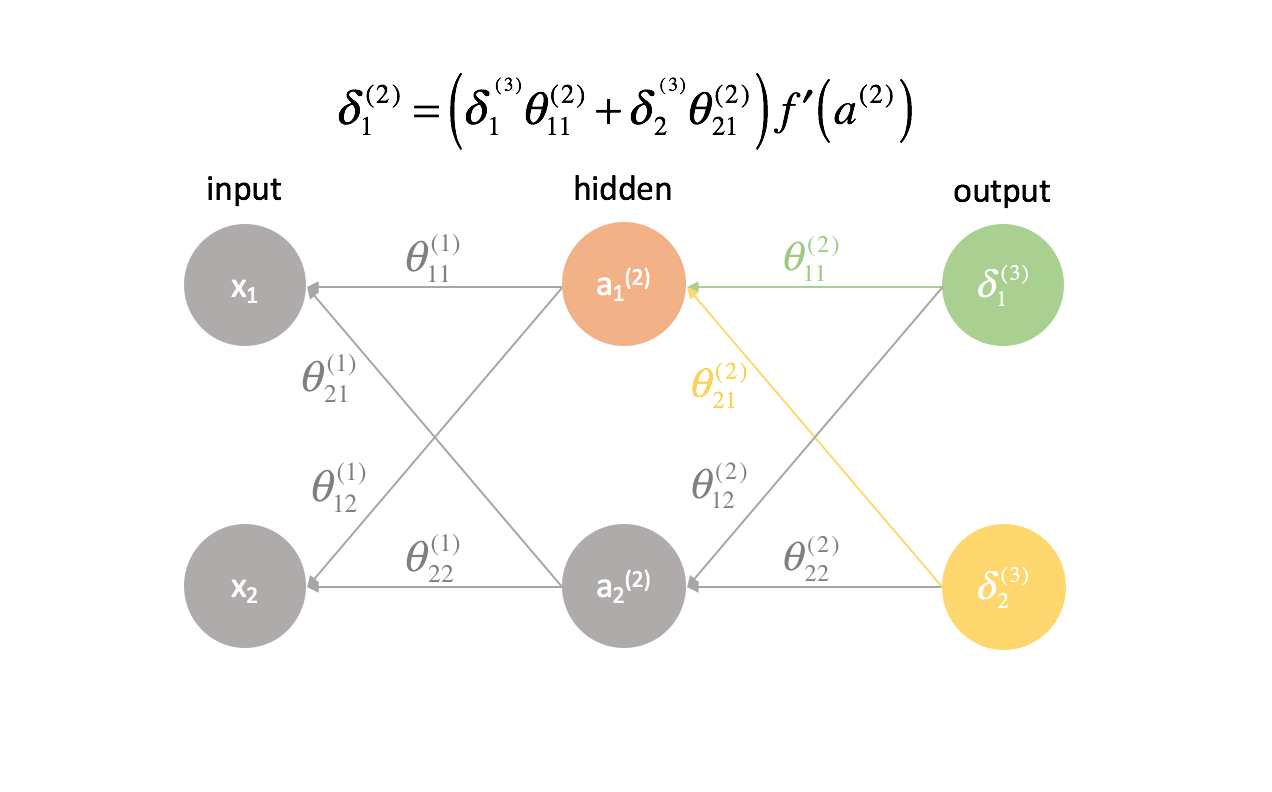
La dernière couche est un cas particulier car nous calculons les valeurs $\delta$ en comparant directement chaque neurone de sortie à sa sortie attendue.
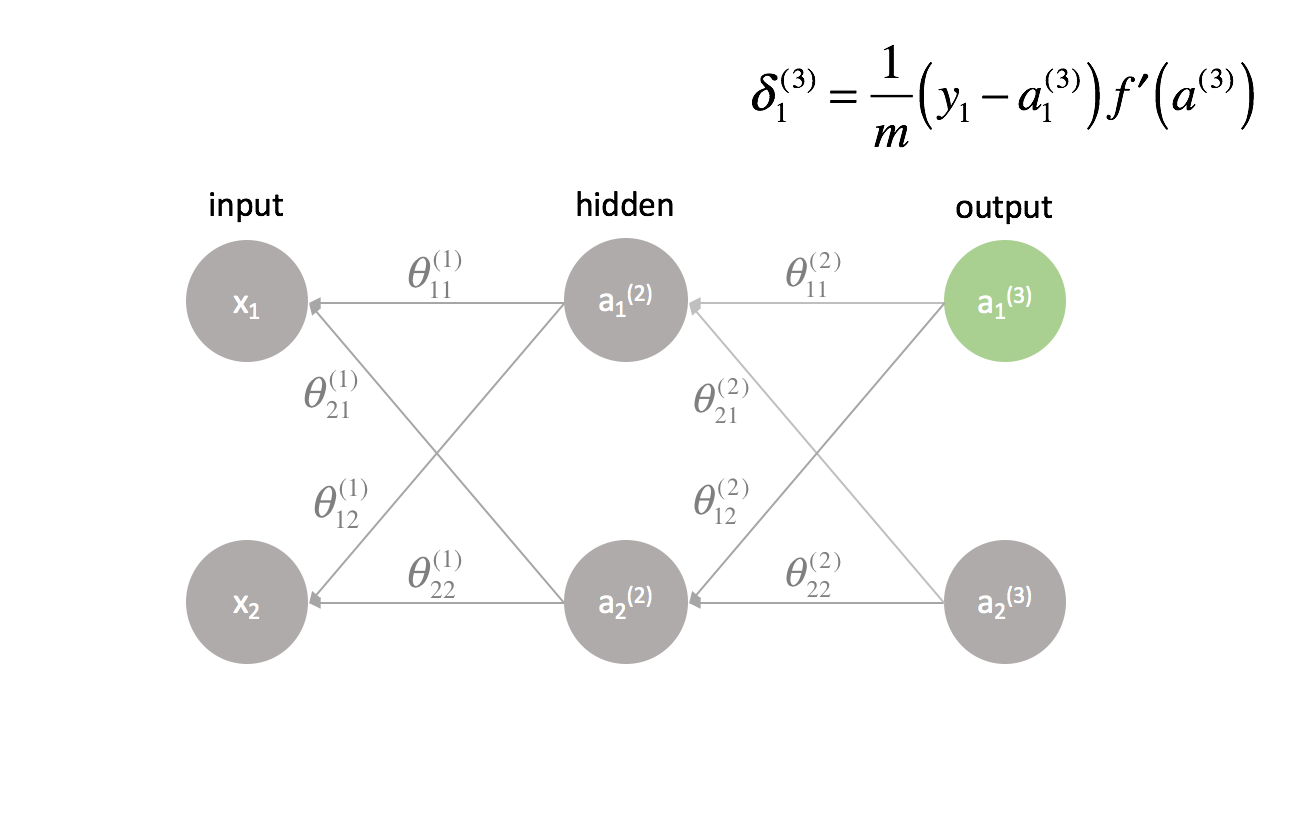
Une méthode formalisée pour mettre en œuvre la rétropropagation
Je vais présenter ici une méthode pratique pour mettre en œuvre la rétropropagation à travers un réseau de couches $l=1,2,…,L$.
-
Exécuter la propagation en avant.
-
Calculer le terme $\delta$ pour la couche de sortie.
-
Calculer les dérivées partielles de la fonction de coût par rapport à tous les paramètres qui alimentent la couche de sortie, ${\Theta ^{(L – 1)}}$.
-
Reculer d’une couche.
$l = l – 1$ -
Calculer le terme $\delta$ pour la couche cachée courante.
-
Calculer les dérivées partielles de la fonction de coût par rapport à tous les paramètres qui alimentent la couche actuelle.
-
Répéter les étapes 4 à 6 jusqu’à atteindre la couche d’entrée.
Réviser l’initialisation des poids
Lorsque nous avons commencé, j’ai proposé que nous initialisions simplement nos poids de manière aléatoire afin d’avoir un point de départ. Cela nous a permis d’effectuer une propagation vers l’avant, de comparer les sorties aux valeurs attendues et de calculer le coût de notre modèle.
Il est en fait très important que nous initialisions nos poids à des valeurs aléatoires afin de pouvoir briser la symétrie de notre modèle. Si nous avions initialisé tous nos poids pour qu’ils soient égaux à être les mêmes, chaque neurone de la couche suivante en avant serait égal à la même combinaison linéaire de valeurs.
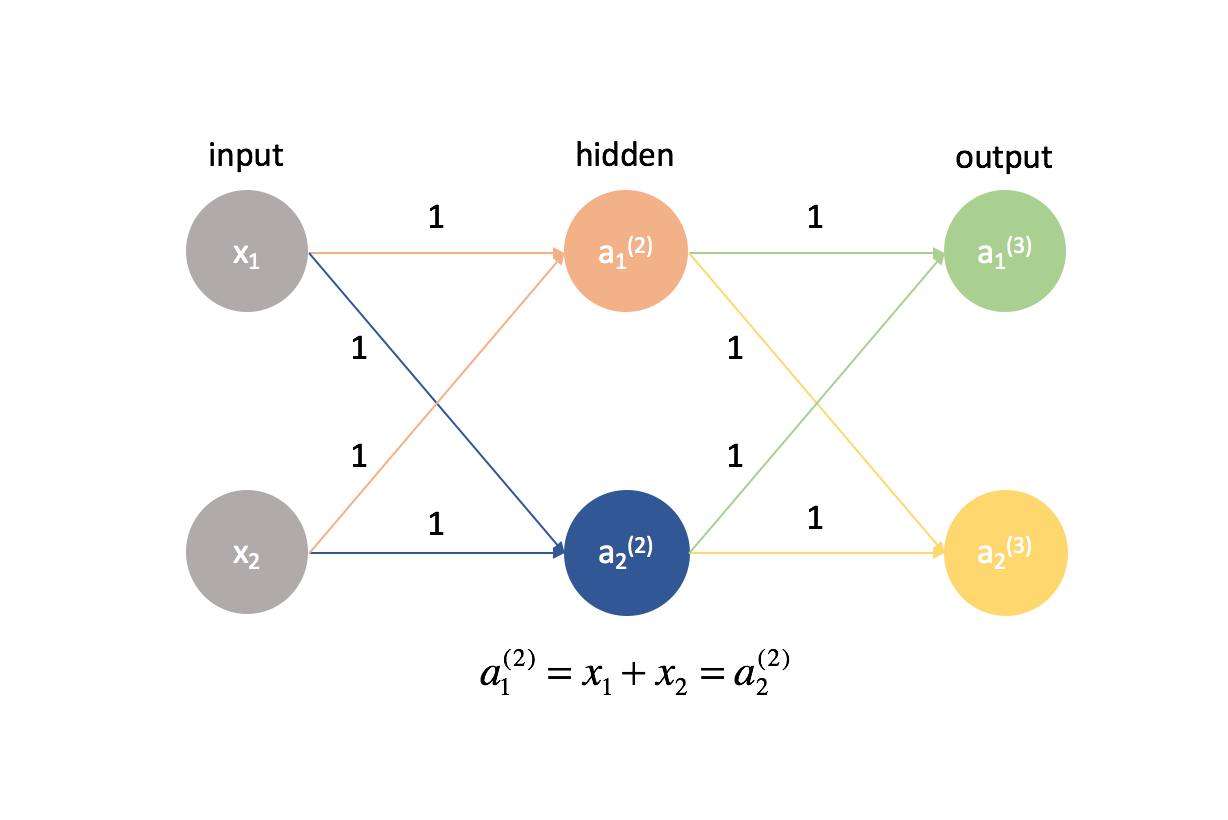
Selon cette même logique, les valeurs de $\delta$ seraient également les mêmes pour chaque neurone d’une couche donnée.
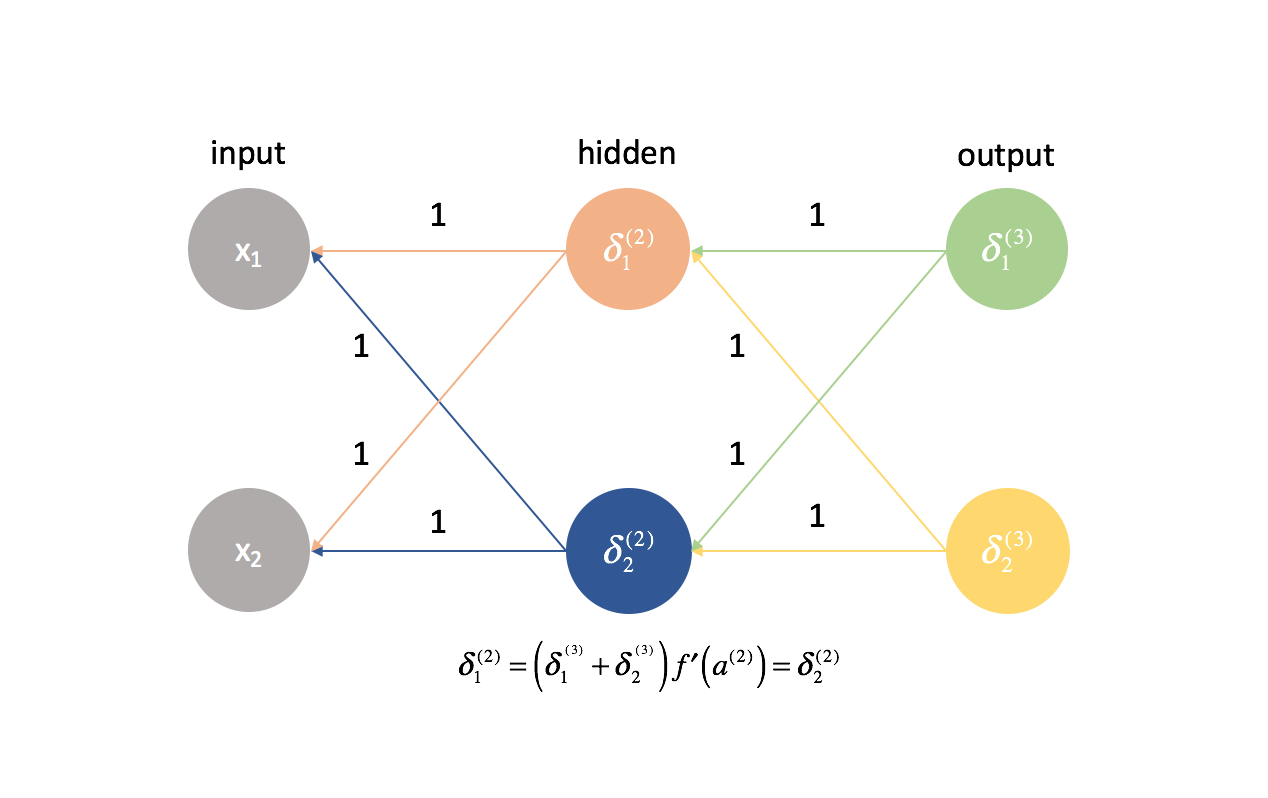
En outre, comme nous calculons les dérivées partielles dans toute couche donnée en combinant les valeurs $\delta$ et les activations, toutes les dérivées partielles dans toute couche donnée seraient identiques. Ainsi, les poids se mettraient à jour de manière symétrique dans la descente de gradient et plusieurs neurones dans une couche quelconque seraient inutiles. Ce ne serait évidemment pas un réseau neuronal très utile.
L’initialisation aléatoire des poids du réseau nous permet de briser cette symétrie et de mettre à jour chaque poids individuellement en fonction de sa relation avec la fonction de coût. Typiquement, nous affecterons chaque paramètre à une valeur aléatoire dans $\left$ où $\varepsilon$ est une certaine valeur proche de zéro.
Mettre tout cela ensemble
Après avoir calculé toutes les dérivées partielles des paramètres du réseau neuronal, nous pouvons utiliser la descente de gradient pour mettre à jour les poids.
En général, nous avons défini la descente de gradient comme
où $\Delta {\theta _i}$ est le « pas » que nous faisons en marchant le long du gradient, mis à l’échelle par un taux d’apprentissage, $\eta$.
Nous utiliserons cette formule pour mettre à jour chacun des poids, recalculer la propagation vers l’avant avec les nouveaux poids, rétropropager l’erreur, et calculer la prochaine mise à jour des poids. Ce processus se poursuit jusqu’à ce que nous ayons convergé vers une valeur optimale pour nos paramètres.
Lors de chaque itération, nous effectuons une propagation vers l’avant pour calculer les sorties et une propagation vers l’arrière pour calculer les erreurs ; une itération complète est appelée une époque. Il est courant de rapporter les métriques d’évaluation après chaque époque afin de pouvoir observer l’évolution de notre réseau neuronal au fur et à mesure de son entraînement.
Lecture complémentaire
-
Le calcul matriciel dont vous avez besoin pour l’apprentissage profond
-
Comment fonctionne l’algorithme de rétropropagation
-
Stanford cs231n : Backpropagation, Intuitions
-
CS231n Hiver 2016 : Cours 4 : Backpropagation, réseaux neuronaux 1
-
Les cours sur le Deep Learning
-
Oui, vous devriez comprendre le backpropagation
-
Blocs de construction des réseaux neuronaux
-
Et au cas où vous venez d’abandonner le backpropagation…. L’apprentissage profond sans backpropagation
.