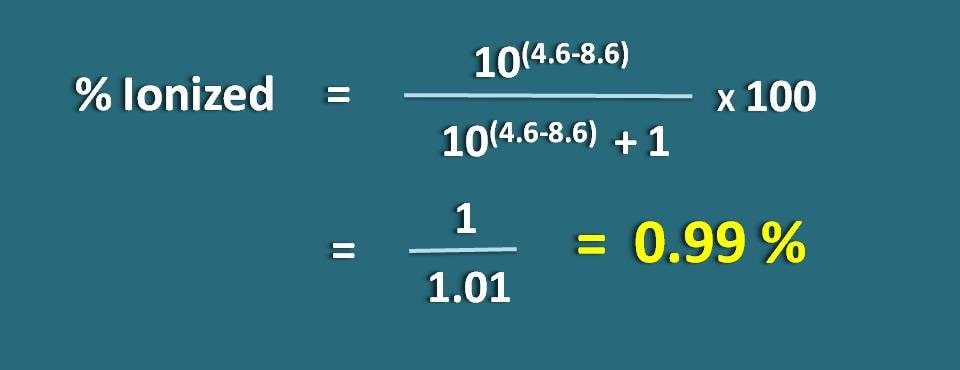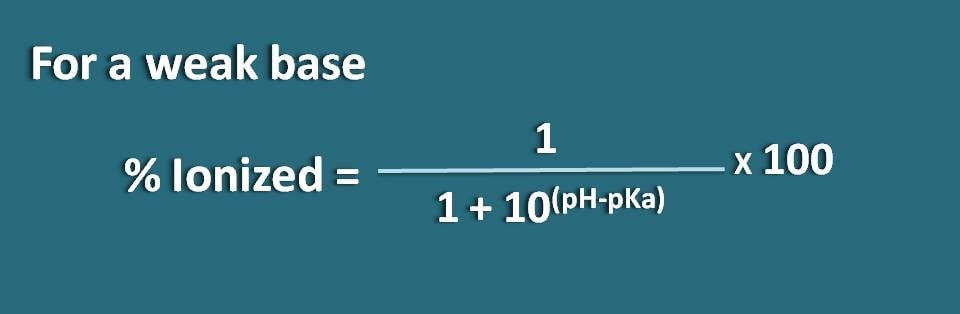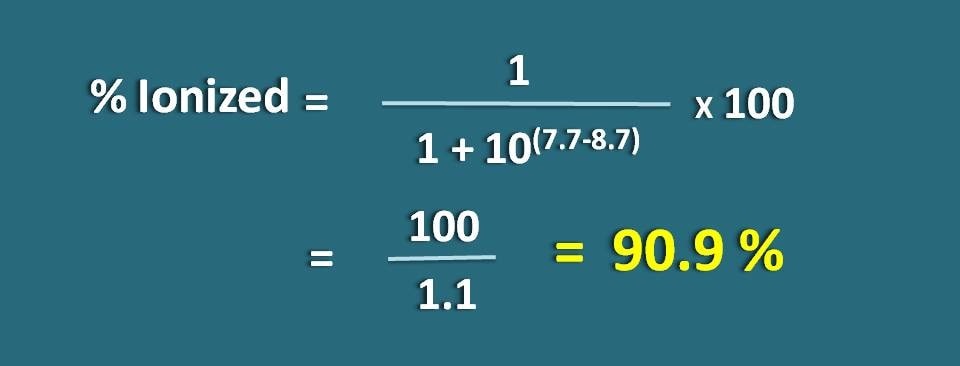有機化合物の物理化学的な特性を評価するために、その化合物のイオン化の状態を知る必要がある場合があります。 例えば、特定のpHでイオン化度が高ければ、水への溶解度も高くなります。
従って、イオン化度の計算は、薬物の薬物動態を扱う際に何度も遭遇する重要な作業です。
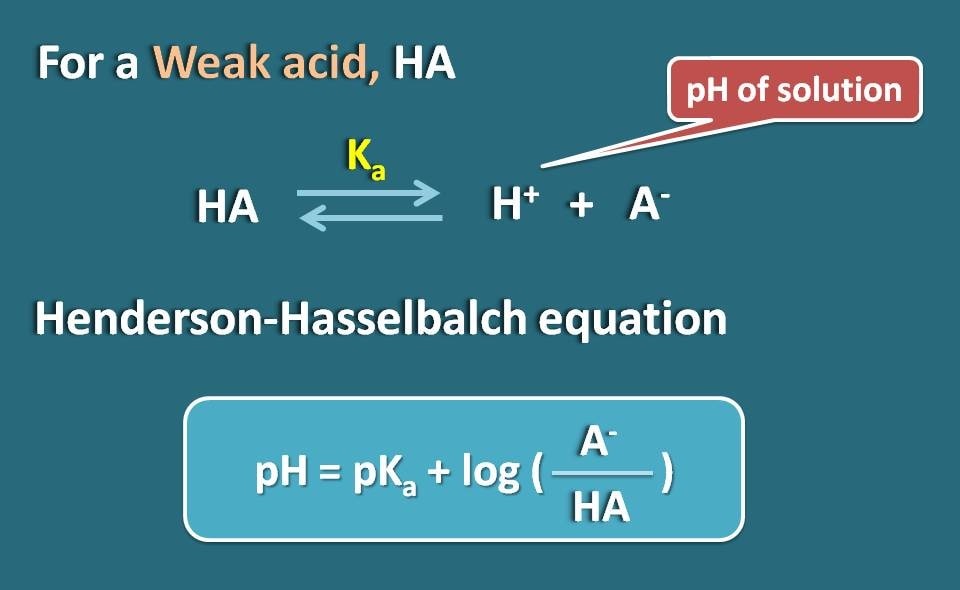
Henderson-Hasselbalch式
弱酸性の働きをするHAのような弱い電解質を考えてみましょう。
Hendersen-Hasselbach方程式を弱酸に適用することで、溶液のpHを薬物のpKaとそのイオン化度に関連付けることができます。
つまり、pH=pKa + log(A-/HA)
ここで、A-は弱酸のイオン化型で、HAは結合型です。
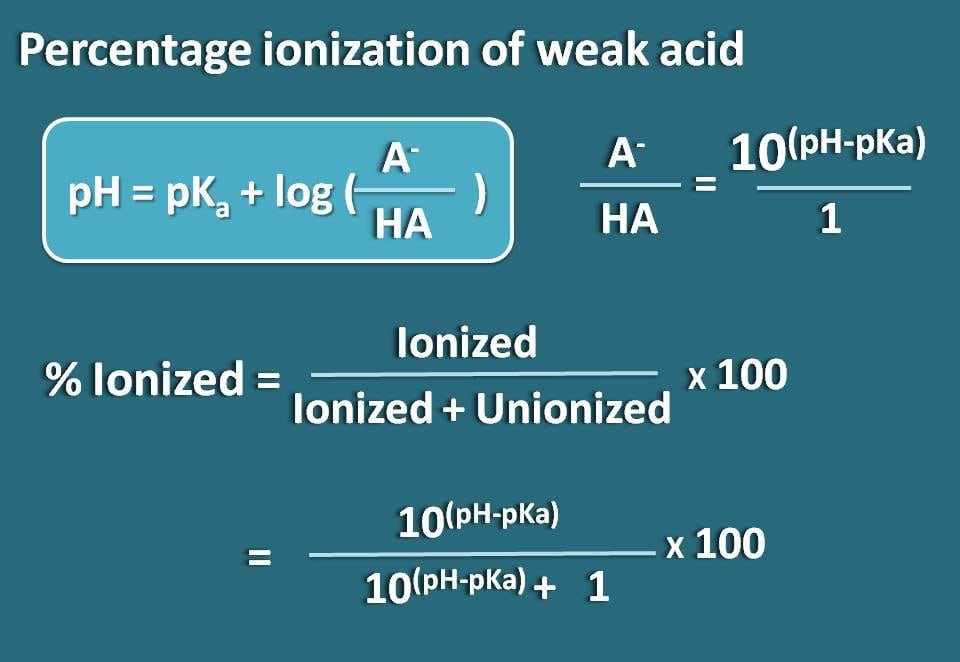
さて、この式をアレンジして、弱酸のイオン化型と結合型の比率を求めてみましょう。
log(A-/HA)=pH – pKa
逆数をとると、
A-/HA=10(pH – pKa)
これで、イオン化体と組合わせ体の比率がわかりました。
% ionized=* 100
この式に代入すると
% ionized=* 100
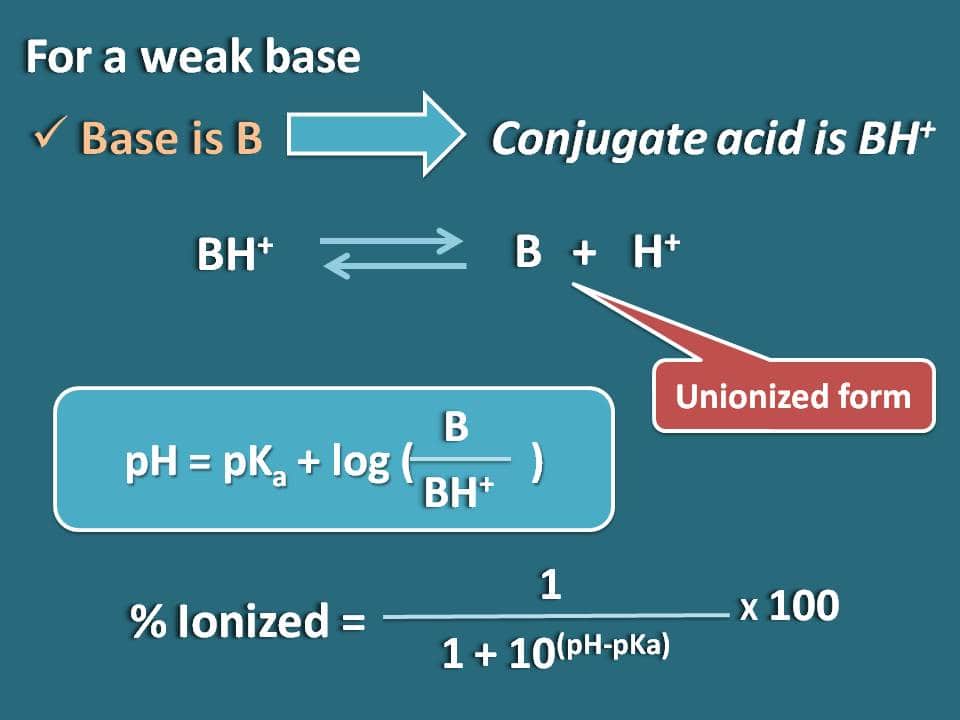
同様に、Bのような弱塩基で共役酸がBH+の場合の式を求めることができます。 ここで、共役酸の化学平衡を以下のように書くことができます。
ここで、共役酸のHendersen-Hasselbalch式を書きます
pH=pKa + log (B/BH+)
ここで、塩基の結合型とイオン化型の比率は次のように書けます
B/BH+=10(pH – pKa)
ここで、結合型の部分は10(pH – pKa)で、イオン化型の部分は1となります。 つまり、イオン化率は
イオン化率=* 100
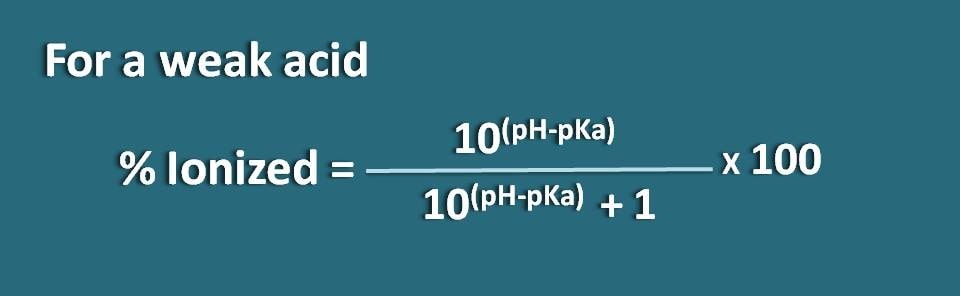
別の方法では、上記の式を再構成することもできます。
% ionized=* 100
さて、いくつかの実用的な例を挙げて、どのように解決するか見てみましょう。
作業例1
pHが4.6でpKa値が8.6の弱酸性の薬物のイオン化率を計算します。
解答:
まず、与えられたデータを列挙します。
pH=4.6、pKa=8.6
弱酸性の薬物なので、以下の式を適用します。
上の式に代入すると、
イオン化率=* 100
=1/1.01=0.99 %
別の例を見てみましょう
作業例2
pH7でイオン化された形の薬物の割合を計算します。
解答:
まず、与えられたデータをリストアップしてみましょう
pH=7.
上の式に置き換えると、
イオン化度=* 100
=100/1.1=90.9 %
最後に別の例題で締めくくります。
作業例3
モルヒネのpKaが7のとき、pH5でプロトン化された形態とプロトン化されていない形態の比率を計算します。
解答:
再び与えられた日付はpH=5、pKa=7です。
モルヒネはオピオイド系の鎮痛剤で、環に3級アミンを持ち、弱塩基として働きます。 プロトン化された形はイオン化された形であり、プロトン化されていない形はユニオン化された形です。 弱塩基の場合、その比率は10(pH – pKa):1となります。
そして、その値を代入してみましょう。
Protonated/ unprotonated=10(5 – 7)/1