De bevelen van de koning zorgen voor een geweldige hersenkraker
(Moeilijkheidsgraad: makkelijk)
Koning Nupe van het koninkrijk Catan is zo dol op zijn twee dochters dat hij besluit dat het koninkrijk beter af zou zijn met meer meisjes dan jongens, en hij vaardigt het volgende decreet uit: Alle paren die kinderen krijgen, moeten kinderen blijven baren tot ze een dochter hebben!
Maar om overbevolking te voorkomen, maakt hij een extra decreet: Alle kinderen dragende paren moeten stoppen met kinderen krijgen zodra ze een dochter hebben! Zijn onderdanen beginnen onmiddellijk zijn bevelen op te volgen.
Na vele jaren, wat is de verwachte verhouding tussen meisjes en jongens in Catan?
Hint
De kans dat elke baby die geboren wordt een meisje is, is natuurlijk 50 procent.
Oplossing
Voorbereid op de oplossing? Klik hier om te zien of je gelijk hebt.
How Many Eggs Does This Hen Lay?
(Moeilijkheidsgraad: Makkelijk)
Dit probleem is ter ere van mijn vader, Harold Feiveson. Dankzij hem ben ik dol op wiskundepuzzels, en dit is een van de eerste problemen (van vele) die hij me gaf toen ik opgroeide.
Een anderhalve kip legt anderhalf ei in anderhalve dag. Hoeveel eieren legt een kip in één dag?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Het wiskundeprobleem met de gouden ketting is bedrieglijk eenvoudig
(Moeilijkheidsgraad: matig)
Je snuffelt op de zolder van je overgrootmoeder als je vijf korte kettinkjes vindt die elk uit vier gouden schakels bestaan. Het komt in je op dat als je ze allemaal samenvoegt tot één grote lus van 20 schakels, je een ongelooflijke ketting zou hebben. Je brengt de ketting naar een juwelier, die je vertelt dat het maken van de ketting 10 dollar kost voor elke gouden schakel die ze moet breken en weer sluiten.
Hoeveel gaat dat kosten?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.
Probeer deze pickleball puzzel op te lossen
(Moeilijkheidsgraad: 🚨HARD🚨)
Kenny, Abby en Ned zijn bij elkaar gekomen voor een round-robin pickleball toernooi, waarbij, zoals gebruikelijk, de winnaar na elk spel overblijft om te spelen tegen de persoon die dat spel uitzat. Aan het eind van hun pickleball-middag is Abby uitgeput, omdat ze de laatste zeven wedstrijden achter elkaar heeft gespeeld. Kenny, die minder vermoeid is, telt de gespeelde games:
Kenny speelde acht games
Abby speelde 12 games
Ned speelde 14 games
Wie won de vierde game tegen wie?
Hint
Hoeveel games zijn er in totaal gespeeld?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Onze Circuit Breaker raadsel is puur kwaad. Sorry.
(Moeilijkheidsgraad: 🚨HARD🚨)
De meterkast van je nieuwe huis zit in een onhandige hoek van je kelder. Tot uw verdriet ontdekt u dat geen van de 100 stroomonderbrekers is voorzien van een label, en u staat voor het afschrikwekkende vooruitzicht om elke stroomonderbreker te koppelen aan het bijbehorende licht. (Veronderstel dat elke stroomonderbreker slechts met één lamp overeenkomt.)
Om te beginnen zet u alle 100 lampen in het huis op “aan”, en vervolgens gaat u naar de kelder om het lastige proces van het in kaart brengen te beginnen. Bij elk bezoek aan je kelder, kun je een willekeurig aantal stroomonderbrekers aan of uit zetten. Vervolgens kun je door de gangen van je huis lopen om te ontdekken welke lampen aan en welke uit zijn.
Wat is het minimumaantal trips dat je naar de kelder moet maken om elke stroomonderbreker bij elk licht in kaart te brengen?
Hint
De oplossing bestaat niet uit het aan- of uitzetten van de lichtschakelaars in uw huis of het voelen hoe heet de gloeilampen zijn. Je zou eerst kunnen proberen op te lossen voor het geval van 10 niet-gelabelde stroomonderbrekers.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Twee Treinen. Twee Oma’s. Kun jij dit lastige wiskunde raadsel oplossen?
(Moeilijkheidsgraad: Matig)
Jesse’s twee oma’s willen hem elk weekend zien, maar ze wonen aan weerszijden van de stad. Als compromis zegt hij dat hij elke zondag op een willekeurig tijdstip naar het dichtstbijzijnde metrostation gaat en op de eerstvolgende trein stapt die aankomt
Als het de trein naar het noorden is, bezoekt hij zijn oma Erica in de stad, en als het de trein naar het zuiden is, bezoekt hij zijn oma Cara in de stad. Zijn beide oma’s vinden dit een goed plan, omdat ze weten dat de treinen in noordelijke en zuidelijke richting elke 20 minuten rijden.
Maar na een paar maanden klaagt oma Cara dat ze hem maar één van de vijf zondagen ziet. Jesse belooft dat hij inderdaad elke dag op een willekeurig tijdstip naar het station gaat. Hoe kan dit?
Hint
De treinen komen altijd op hun geplande tijden.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Hier is een echt F@*#ing moeilijk wiskundeprobleem over mieren
(Moeilijkheidsgraad: 🚨HARD🚨)
Max en Rose zijn mierenbroers en -zussen. Ze houden ervan om tegen elkaar te racen, maar ze spelen altijd gelijk, omdat ze eigenlijk met precies dezelfde snelheid kruipen. Dus besluiten ze een race te houden waarbij een van hen (hopelijk) zal winnen.
Voor deze race begint elk van hen in de onderste hoek van een kubus, en kruipt dan zo snel als ze kunnen om een kruimel in de tegenoverliggende hoek te bereiken. De afmetingen van hun kubussen zijn zoals afgebeeld:
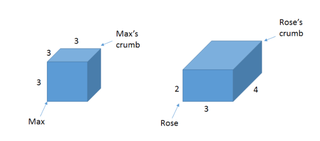
Als ze allebei de kortst mogelijke route nemen om hun kruimel te bereiken, wie zal dan als eerste zijn kruimel bereiken? (Vergeet niet dat het mieren zijn, dus ze kunnen natuurlijk overal op de randen of het oppervlak van de kubus klimmen.)
Hint
Bedenk: Denk buiten de doos.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.
Dit Peppermint Patty raadsel is praktisch onmogelijk
(Moeilijkheidsgraad: 🚨HARD🚨)
Je staat tegenover je vriendin, Caryn, in een “candy-off”, die als volgt werkt: Er ligt een stapel van 100 caramels en één pepermuntvlaai. Jij en Caryn gaan heen en weer en nemen in elke beurt ten minste één en niet meer dan vijf caramels van de snoepstapel. Degene die de laatste karamel weghaalt, krijgt ook het pepermuntvlaaitje. En jij houdt van pepermuntvla.
Voorstel dat Caryn jou laat beslissen wie er eerst gaat. Wie moet je kiezen om er zeker van te zijn dat je de pepermunt patty wint?
Hint
Vorstel eerst een stapel van 10 karamels.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Kun jij het Grote Amerikaanse Rail-Trail Raadsel oplossen?
(Moeilijkheidsgraad: Matig)
Dit probleem werd voorgesteld door de natuurkundige P. Jeffrey Ungar.
Eindelijk is de Grote Amerikaanse Rail-Trail door het hele land voltooid! Klop jezelf maar op de borst: je hebt zojuist de langste leuning in de geschiedenis van de wereld aangelegd, met een afstand van 4000 mijl van begin tot eind. Maar net na de openingsceremonie herinnert uw assistent u eraan dat het metaal dat u voor de leuning hebt gebruikt in de zomer iets uitzet, zodat de lengte in totaal met één centimeter zal toenemen.
“Ha!” zegt u, “Eén centimeter in een leuning van 4.000 mijl? Dat is niets!” Maar… heeft u gelijk?
Laten we eens aannemen dat als de leuning uitzet, hij op zijn zwakste punt, in het midden, naar boven knikt. Hoeveel hoger moeten voetgangers in het midden van het land in de zomer reiken om de leuning vast te pakken? Dat wil zeggen, in de onderstaande figuur, wat is h? (Negeer in deze vraag de kromming van de aarde en ga ervan uit dat het pad een rechte lijn is.)
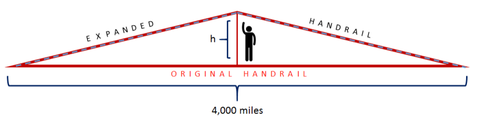
Hint
Pythagoras is een fascinerende historische figuur.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Dit raadsel is als een bijzonder wreed SAT-probleem. Kun jij het antwoord vinden?
(Moeilijkheidsgraad: gemiddeld)
Amanda woont met haar tienerzoon Matt op het platteland – een autoritje verwijderd van Matt’s school. Elke middag verlaat Amanda het huis op hetzelfde tijdstip, rijdt met constante snelheid naar de school, haalt Matt precies op als zijn schaakclub om 17.00 uur is afgelopen, en dan gaan ze meteen samen met dezelfde constante snelheid terug naar huis. Maar op een dag voelt Matt zich niet goed, dus verlaat hij de schaakles eerder en gaat op zijn draagbare scooter naar huis.
Nadat Matt een uur heeft gescooterd, komt Amanda hem tegen in haar auto (op haar gebruikelijke route om hem op te halen), en ze keren samen terug, waarbij ze 40 minuten eerder thuiskomen dan ze gewoonlijk doen. Hoeveel schaaktraining heeft Matt gemist?
Hint
Bedenk het geval waarin Amanda Matt precies tegenkomt op het moment dat ze hun huis verlaat.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.
Kun jij deze 3 filmsterren over de rivier krijgen?
(Moeilijkheidsgraad: Matig)
Drie filmsterren, Chloe, Lexa, en Jon, zijn een film aan het opnemen in het Amazonegebied. Ze zijn erg beroemd en zeer onderhoudend, dus hun agenten zijn altijd bij hen. Op een dag, na het filmen van een scène diep in het regenwoud, besluiten de drie acteurs en hun agenten te voet terug te gaan naar hun thuisbasis. Plotseling komen ze bij een grote rivier.
Op de oever van de rivier vinden ze een kleine roeiboot, maar die is maar groot genoeg voor twee personen tegelijk. Het addertje onder het gras? Geen van de agenten vindt het prettig om hun filmster bij andere agenten achter te laten als zij er niet ook bij zijn. Ze vertrouwen er niet op dat de andere agenten niet zullen proberen hun ster weg te kapen.
Bijvoorbeeld, Chloe’s agent vindt het prima als Chloe en Lexa alleen in de boot of op een van de rivieroevers zijn, maar absoluut niet als Lexa’s agent ook bij hen is. Dus hoe kunnen ze allemaal aan de overkant van de rivier komen?
Hint
Er is niet maar één manier om dit probleem op te lossen.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Dit belachelijk moeilijke raadsel is ons eerbetoon aan een overleden wiskundig genie. Kun jij het oplossen?
(Moeilijkheidsgraad: 🚨HARD🚨)
Op 11 april overleed John Horton Conway, een briljant wiskundige die een intense en speelse liefde voor puzzels en spelletjes had, aan de complicaties van COVID-19. Conway is de uitvinder van een van mijn favoriete legendarische problemen (niet voor de zwakkeren van hart) en, beroemd geworden, het Spel van het Leven. Ik heb dit probleem ter ere van hem gemaakt.
Carol was een stamboom aan het maken, maar had moeite om de geboortedatum van haar moeder te achterhalen. De enige aanwijzing die ze vond was een brief van haar grootvader aan haar grootmoeder op de dag dat haar moeder werd geboren. Helaas waren sommige letters uitgevaagd, hier weergegeven met een “___”. (De lengte van de regel geeft niet het aantal uitgevlekte tekens weer.)
“Lieve Virginia,
Toen ik maandagmorgen naar mijn werk ging, wist ik nog niet dat we tegen de avond een prachtig meisje zouden krijgen. En nog wel op onze trouwdag! Het doet me terugdenken aan die ongelooflijke weekenddag, 27 juli 1941, toen we voor het eerst onze gelofte aflegden om samen een gezin te stichten, en hier zijn we dan! Gelukkige achtste verjaardag, mijn liefde.
Liefde, Edwin”
De vraag: Wanneer is Carols moeder geboren?
Hint
Dit probleem is geïnspireerd op Conway’s Doomsday Rule.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Om dit ingewikkelde wiskundige raadsel op te lossen, heb je maar één riem en één aarde nodig
(Moeilijkheidsgraad: gemiddeld)
Stel je voor dat je een heel lange riem hebt. Nou ja, extreem lang, eigenlijk … in feite is hij net lang genoeg om de omtrek van onze hele planeet te omsluiten. (Laten we voor het gemak aannemen dat de aarde perfect rond is, zonder bergen, oceanen of andere obstakels in de weg van de gordel.)
Natuurlijk ben je erg trots op je gordel. Maar dan komt je broer, Peter, en tot je ongenoegen komt hij met een riem die net iets langer is dan die van jou. Hij schept op dat zijn riem langer is dan zijn lengte: 1,80 meter.
Als Peter zijn riem ook om de omtrek van de Aarde zou wikkelen, hoe ver zou hij de riem dan boven het oppervlak kunnen laten zweven als hij er strak en gelijkmatig aan zou trekken?
Hint
De omtrek van de Aarde is ongeveer 25.000 mijl, of 130 miljoen voet … maar dat hoef je niet te weten om dit probleem op te lossen.
Oplossing
Voorbereid op de oplossing? Klik hier om te zien of je gelijk hebt.
Dit elleboogtikraadsel is duivels. Good Luck Solving It.
(Moeilijkheidsgraad: 🚨HARD🚨)
In een toekomstige tijd, wanneer het verbod op schuilplaatsen wordt opgeheven, gaat een getrouwd stel, Florian en Julia, naar een bar om hun pas verworven vrijheid te vieren.
Ze vinden daar vier andere stellen die hetzelfde idee hadden.
Gretig op zoek naar sociaal contact, tikt iedereen van de vijf stellen enthousiast ellebogen (de nieuwe handdruk) met elke persoon die ze nog niet hebben ontmoet.
Het blijkt dat veel van de mensen elkaar al kenden, dus als Julia aan iedereen vraagt hoeveel ellebogen ze hebben getikt, krijgt ze opmerkelijk genoeg negen verschillende antwoorden!
De vraag: Hoeveel ellebogen heeft Florian getikt?
Hint
Welke negen antwoorden heeft Julia gehoord?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Je hebt een borrel nodig na het oplossen van dit whiskyraadsel
(Moeilijkheidsgraad: Makkelijk)
Alan en Claire leven volgens het oude Schotse gezegde: “Drink nooit whisky zonder water, en ook geen water zonder whisky!” Dus op een dag, als Alan een glas whisky voor zich heeft en Claire een glas water van dezelfde grootte, neemt Alan een lepel van zijn whisky en doet die in Claire’s water.
Claire roert haar met whisky getinte water, en doet dan een lepel van dit mengsel terug in Alan’s whisky om er zeker van te zijn dat ze precies evenveel te drinken hebben.
Dus: Zit er meer water in Alan’s whisky, of meer whisky in Claire’s water? En maakt het uit hoe goed Claire roert?
Hint
De grootte van de lepel doet er niet toe.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Het Doodleprobleem is veel moeilijker dan het lijkt. Kun jij het oplossen?
(Moeilijkheidsgraad: Matig)
Het raadsel van deze week is relatief eenvoudig, maar toch sinister.
De vraag: Kun je 100 maken door een willekeurig aantal plussen en minnen in de reeks cijfers 9 8 7 6 5 4 3 2 1 te zetten? Je kunt de volgorde van de cijfers niet veranderen! Dus wat is het kleinste aantal plussen en minnen dat nodig is om 100 te maken?
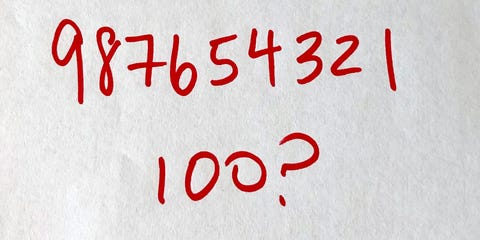
Het getal 98 – 7 – 6 + 54 – 32 is bijvoorbeeld een manier om plussen en minnen door elkaar te laten lopen, maar omdat het gelijk is aan 107, is het geen oplossing.
Ik noem dit een “doodle-probleem”: een probleem waar je het beste aan kunt werken tijdens vergaderingen waar je anders aan het krabbelen zou zijn.
Hint
Je zou kunnen beginnen met het zoeken naar oplossingen die in totaal zeven plussen en minnen gebruiken (hoewel er manieren zijn om er minder te gebruiken).
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Deze wiskundepuzzel heeft op één na alle wetenschappers versteld doen staan. Denk je dat jij hem kunt kraken?
(Moeilijkheidsgraad: HARD)
Ter ere van Freeman Dyson, de beroemde natuurkundige die vorige maand overleed, hier een legendarisch verhaal dat zijn gevatheid en ongelooflijke denkkracht demonstreert.
Op een dag vroeg een van de topwetenschappers zich hardop af of er een geheel getal bestaat dat je precies kunt verdubbelen door het laatste cijfer naar voren te schuiven. Bijvoorbeeld 265 zou hieraan voldoen als 526 het exacte dubbelgetal zou zijn – wat niet het geval is.
Na kennelijk slechts vijf seconden antwoordde Dyson: “Natuurlijk bestaat dat, maar het kleinste getal van die aard heeft 18 cijfers.”
Daarop vroegen enkele van de slimste wetenschappers ter wereld zich af hoe hij dit zo snel had kunnen bedenken.
Dus, gezien Dysons hint, wat is het kleinste getal van die aard?
Hint
Mijn tweedeklasser heeft onlangs geleerd hoe je een getal van 3 cijfers bij zichzelf optelt met de klassieke verticale methode:

18-cijferige getallen kunnen natuurlijk op dezelfde manier worden opgeteld.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je het goed hebt.
Bedenk wat er op haar voorhoofd staat
(Moeilijkheidsgraad: Matig)
Cecilia houdt ervan om de logica van haar zeer logische vrienden Jaya, Julian en Levi op de proef te stellen, dus kondigt ze aan:
“Ik schrijf een positief getal op elk van jullie voorhoofden. Geen van de getallen is hetzelfde, en twee van de getallen tellen op tot het derde.”
Ze krabbelt de getallen op hun hoofden, draait zich dan naar Jaya en vraagt haar wat haar nummer is. Jaya ziet dat Julian 20 op zijn voorhoofd heeft, en Levi 30 op het zijne. Ze denkt even na en zegt dan: “Ik weet niet wat mijn nummer is.” Julian zegt: “Ik weet mijn nummer ook niet,” en dan roept Levi uit: “Ik ook niet!” Cecilia zegt vrolijk: “Ik heb jullie eindelijk door!”
“Niet zo snel!” Zegt Jaya. “Nu weet ik mijn nummer!”
Wat is Jaya’s nummer?
Hint
Jaya zou een van de twee nummers kunnen zijn, maar slechts een van die nummers zou ertoe leiden dat Julian en Levi allebei hun nummer niet weten. Waarom?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.
Kan jij Keanu Reeves tot president laten kiezen?
(Moeilijkheidsgraad: Matig)
Het is 2024 en er zijn vijf kandidaten voor de democratische voorverkiezing: Taylor Swift, Oprah Winfrey, Mark Cuban, Keanu Reeves, en Dwayne Johnson. (Hé, het zou kunnen.) Zoals gebruikelijk is de eerste voorverkiezing in Iowa.
In een poging om de schaamte na het caucus-debacle van 2020 te overwinnen, heeft de Democratische Partij van Iowa zojuist een nieuwe, onfeilbare manier aangekondigd om de beste kandidaat te vinden: er zullen vier opeenvolgende verkiezingen zijn.
Eerst zal kandidaat 1 het opnemen tegen kandidaat 2. Vervolgens neemt de winnaar het op tegen kandidaat 3, dan neemt de winnaar het op tegen kandidaat 4, en tenslotte neemt de winnaar het op tegen de laatste kandidaat. Door de transitieve eigenschap moet de winnaar van deze laatste verkiezing de beste kandidaat zijn … zo zegt de Democratische Partij van Iowa.
Kandidaat Keanu voelt zich behoorlijk down, omdat hij weet dat hij door de meeste kiezers bijna onderaan staat, en door niemand bovenaan. In feite weet hij dat de bevolking van Iowa is verdeeld in vijf gelijke groepen, en dat hun voorkeuren als volgt zijn:

Keanu is jeugdvrienden met Bill S. Preston, Esq., het nieuwe hoofd van de Iowa Democratische Partij. Preston, ervan overtuigd dat de volgorde van de kandidaten niet uitmaakt voor de uitslag, vertelt Keanu dat hij de stemvolgorde van de kandidaten mag bepalen.
Welke volgorde moet Keanu kiezen?
Hint
Hoe zou het Keanu vergaan in een één-op-één race tegen elke kandidaat?
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.
Wie heeft al die verdomde kluisjes opengemaakt?
(Moeilijkheidsgraad: Matig)
Er staan 100 kluisjes in de gang van de Chelm High School. Elke avond zorgt de schooldirecteur ervoor dat alle kastjes gesloten zijn, zodat de volgende dag ordelijk kan beginnen. Op een dag besluiten 100 ondeugende leerlingen een grap uit te halen.
De leerlingen verzamelen zich voordat de school begint en gaan in de rij staan. De eerste leerling loopt door de gang en opent elk kastje. De volgende leerling volgt en sluit alle andere kastjes (te beginnen bij het tweede kastje). Leerling 3 gaat dan naar elk derde kastje (beginnend bij het derde) en opent het als het dicht is, en sluit het als het open is. Leerling 4 opent vervolgens elk vierde kastje als het dicht is en sluit het als het open is. Zo gaat het maar door tot leerling 100 uiteindelijk bij het honderdste kastje is. Als de directrice later op de ochtend aankomt, welke kastjes vindt ze dan open?
Hint
Zorg ervoor dat je aandacht besteedt aan alle factoren.
Oplossing
Klaar voor de oplossing? Klik hier om te zien of je gelijk hebt.