Heading

In mijn eerste bericht over neurale netwerken besprak ik een modelweergave voor neurale netwerken en hoe we ingangen kunnen invoeren en een uitvoer kunnen berekenen. We berekenden deze uitvoer, laag voor laag, door de ingangen van de vorige laag te combineren met gewichten voor elke neuron-neuronverbinding. Ik heb gezegd dat we in een volgende post zouden bespreken hoe we de juiste gewichten kunnen vinden om neuronen met elkaar te verbinden – dit is die post!

Overzicht

In de vorige post ging ik ervan uit dat we magische voorkennis hadden over de juiste gewichten voor elk neuraal netwerk. In dit artikel gaan we uitzoeken hoe we ons neurale netwerk de juiste gewichten kunnen laten “leren”. Maar om ergens te kunnen beginnen, initialiseren we de gewichten met willekeurige waarden als een eerste gok. We zullen later in dit artikel terugkomen op deze willekeurige initialisatiestap.

Gezien onze willekeurig geïnitialiseerde gewichten die alle neuronen verbinden, kunnen we nu onze matrix van waarnemingen invoeren en de uitgangen van ons neurale netwerk berekenen. Dit wordt forward propagation genoemd. Aangezien we onze gewichten willekeurig hebben gekozen, zal onze output waarschijnlijk niet erg goed zijn ten opzichte van de verwachte output voor de dataset.

Dus hoe gaan we nu verder?

Wel, om te beginnen, laten we eens definiëren hoe een “goede” output eruit ziet. We ontwikkelen een kostenfunctie die uitvoer die ver van de verwachte waarde ligt, afstraft.

Daarna moeten we een manier vinden om de gewichten te veranderen, zodat de kostenfunctie verbetert. Elk pad van een input-neuron naar een output-neuron is in wezen slechts een samenstelling van functies; als zodanig kunnen we gedeeltelijke afgeleiden en de kettingregel gebruiken om de relatie tussen elk gegeven gewicht en de kostenfunctie te definiëren. Deze kennis kunnen we vervolgens gebruiken om de gradiënt-afname te gebruiken bij het bijwerken van elk van de gewichten.

Voorwaarden

Toen ik voor het eerst backpropagation leerde, probeerden veel mensen de onderliggende wiskunde (afgeleide ketens) weg te abstraheren en ik was nooit echt in staat om te begrijpen wat er aan de hand was, totdat ik de lezing van professor Winston op MIT zag. Ik hoop dat dit artikel een beter begrip geeft van backpropagation dan “dit is de stap waarin we de fout terugsturen om de gewichten bij te werken”.

Om de concepten die in dit artikel worden besproken volledig te kunnen begrijpen, moet je met het volgende bekend zijn:

Partiële afgeleiden
Dit artikel zal een beetje te uitgebreid zijn met een heleboel gedeeltelijke afgeleiden. Ik hoop echter dat zelfs een lezer zonder voorkennis van multivariate calculus de logica achter backpropagation kan volgen.

Als je niet bekend bent met calculus, dan zal $\frac{{{partiële f\left( x \right)}}{{{partiële x}}$ je waarschijnlijk nogal vreemd voorkomen. Je kunt deze uitdrukking interpreteren als: “Hoe verandert $f1-links( x-rechts)$ als ik $x$ verander?” Dit is nuttig omdat we dan vragen kunnen stellen als “Hoe verandert de kostenfunctie als ik deze parameter verander? Verhoogt of verlaagt de kostenfunctie?” op zoek naar de optimale parameters.

Als je de multivariate calculus wilt bijspijkeren, bekijk dan de lessen van Khan Academy over dit onderwerp.

Gradiënt afdaling
Om te voorkomen dat deze post te lang wordt, heb ik het onderwerp gradiënt afdaling in een andere post behandeld. Als je niet bekend bent met de methode, lees er dan eerst over voordat je verder gaat met deze post.

Matrixvermenigvuldiging
Hier een snelle opfrisser van Khan Academy.

Start eenvoudig

Om uit te vinden hoe je gradient descent gebruikt bij het trainen van een neuraal netwerk, laten we beginnen met het eenvoudigste neurale netwerk: één input neuron, één verborgen laag neuron, en één output neuron.

Om een vollediger beeld te geven van wat er gebeurt, heb ik elk neuron uitgebreid om 1) de lineaire combinatie van ingangen en gewichten en 2) de activering van deze lineaire combinatie weer te geven. Het is gemakkelijk te zien dat de voorwaartse voortplantingsstap eenvoudigweg een reeks functies is waarbij de output van de ene als input voor de volgende wordt gebruikt.

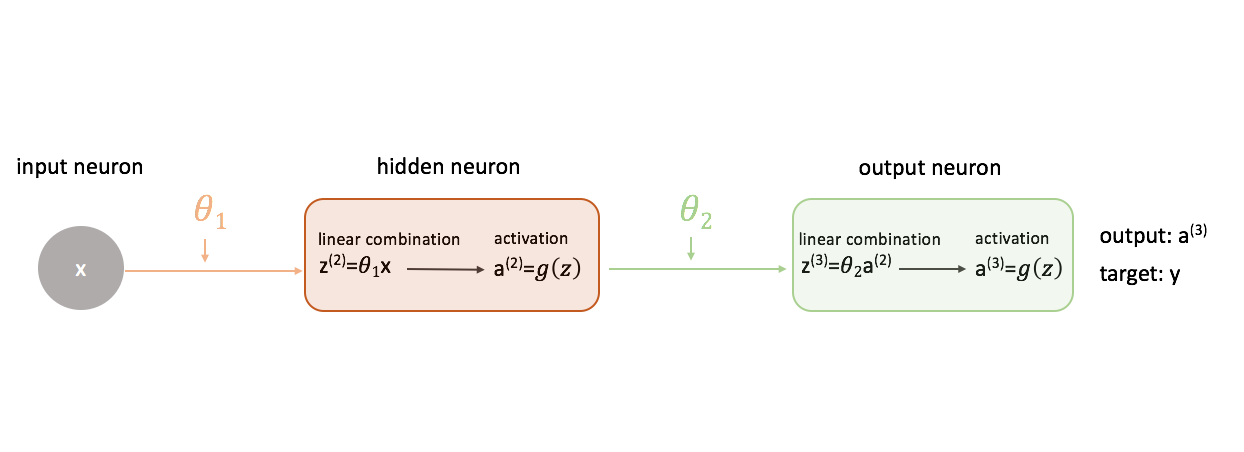
Het definiëren van “goede” prestaties in een neuraal netwerk

Laten we onze kostenfunctie eenvoudigweg definiëren als de gekwadrateerde fout.

Er zijn talloze kostenfuncties die we zouden kunnen gebruiken, maar voor dit neurale netwerk werkt de gekwadrateerde fout prima.

Bedenk dat we de output van ons model ten opzichte van de doeloutput willen evalueren in een poging het verschil tussen die twee te minimaliseren.

Het relateren van de gewichten aan de kostenfunctie

Om het verschil tussen de output van ons neurale netwerk en de doeloutput te minimaliseren, moeten we weten hoe de prestaties van het model veranderen ten opzichte van elke parameter in ons model. Met andere woorden, we moeten de relatie (lees: gedeeltelijke afgeleide) tussen onze kostenfunctie en elk gewicht definiëren. Vervolgens kunnen we deze gewichten bijwerken in een iteratief proces met behulp van gradiënt-afdaling.

Laten we eerst eens kijken naar $

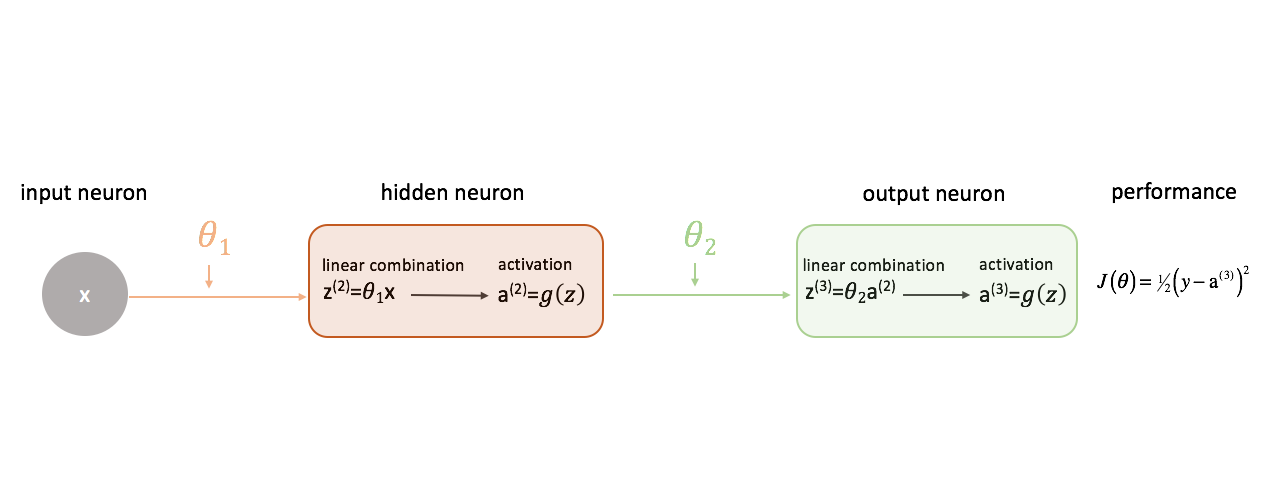
Laten we eens kijken hoe we het verband tussen $J\left( \theta \right)$ en $\theta _2$ zouden kunnen uitdrukken. Merk op hoe $\theta _2$ een ingang is voor ${z^{(3)}}$, die een ingang is voor ${{\rm{a}}^{(3)}}$, die een ingang is voor $J\left( \theta \rechts)$. Als we zo’n afgeleide proberen te berekenen, kunnen we de kettingregel gebruiken om op te lossen.

Als geheugensteuntje, de kettingregel luidt:

Laten we de kettingregel toepassen om op te lossen voor $J\left( \theta \rechts)}}{\left {\theta _2}}}$.

Op dezelfde manier kunnen we $\frac{\left J\left( \theta \right)}}{{\left {\theta _1}}$ vinden.

Voor de duidelijkheid heb ik ons neurale netwerk diagram aangepast om deze ketens te visualiseren. Zorg ervoor dat u vertrouwd bent met dit proces voordat u verdergaat.

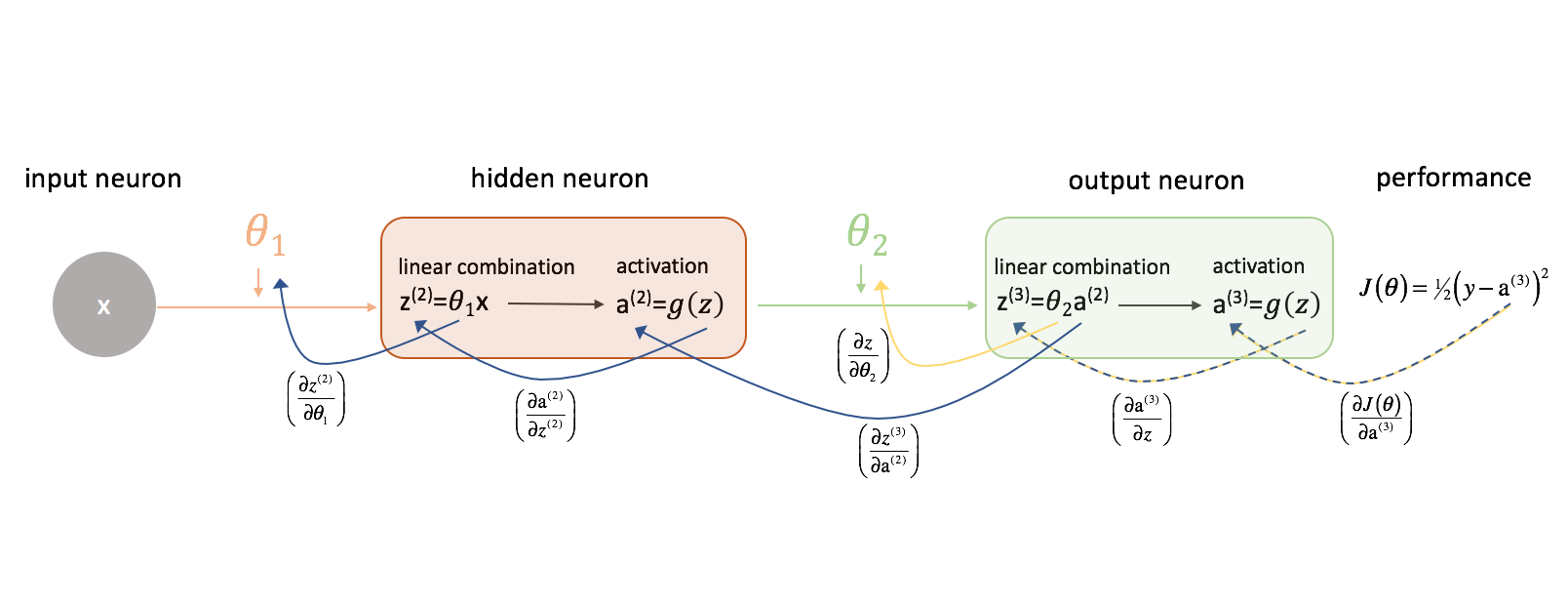
Vergroot de complexiteit

Nu gaan we dezelfde aanpak op een iets gecompliceerder voorbeeld uitproberen. We bekijken een neuraal netwerk met twee neuronen in de inputlaag, twee neuronen in de verborgen laag, en twee neuronen in de outputlaag. Voorlopig laten we de neuronen die ontbreken in de input- en verborgen lagen buiten beschouwing.

Laten we even stilstaan bij de notatie die ik zal gebruiken, zodat u deze diagrammen kunt volgen. Het superscript (1) geeft aan in welke laag het object zich bevindt en het subscript geeft aan naar welk neuron in een bepaalde laag we verwijzen. Bijvoorbeeld $a_1^{(2)}$ is de activatie van het eerste neuron in de tweede laag. De parameterwaarden $theta$ lees ik graag als een mailing label – de eerste waarde geeft aan naar welk neuron de input in de volgende laag wordt gestuurd, en de tweede waarde geeft aan van welk neuron de informatie wordt gestuurd. Bijvoorbeeld, ${{21}^{(2)}}$ wordt gebruikt om input naar het 2e neuron te sturen, vanaf het 1e neuron in laag 2. Het superscript dat de laag aanduidt, correspondeert met waar de input vandaan komt. Deze notatie is consistent met de matrixrepresentatie die we hebben besproken in mijn post over de representatie van neurale netwerken.

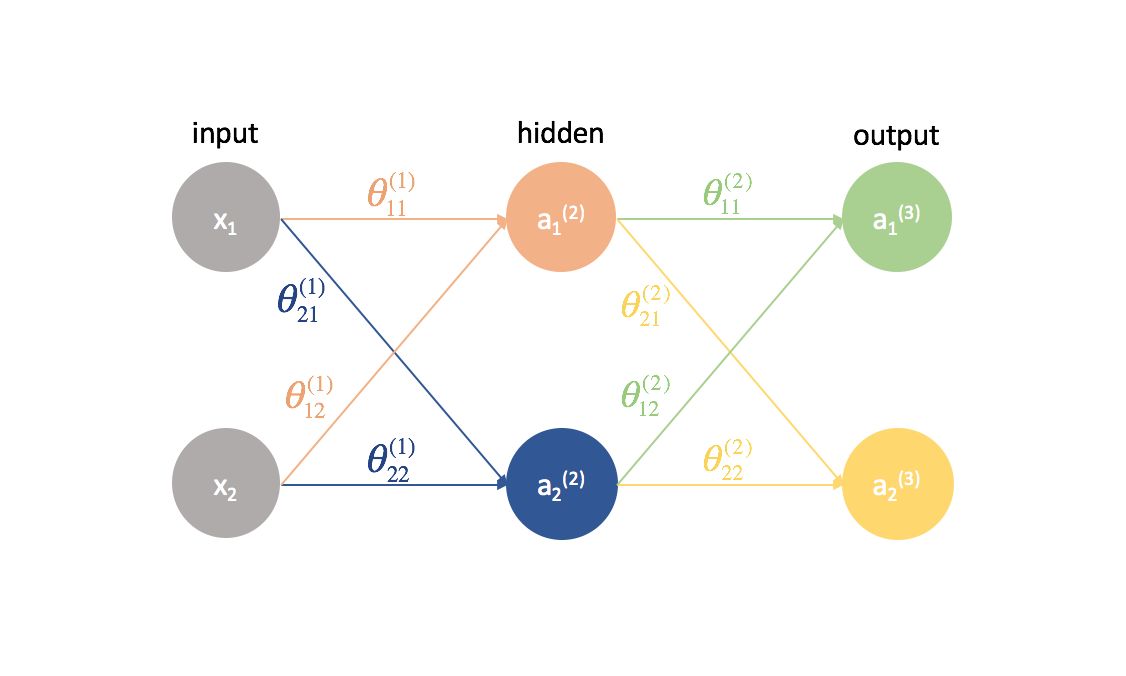
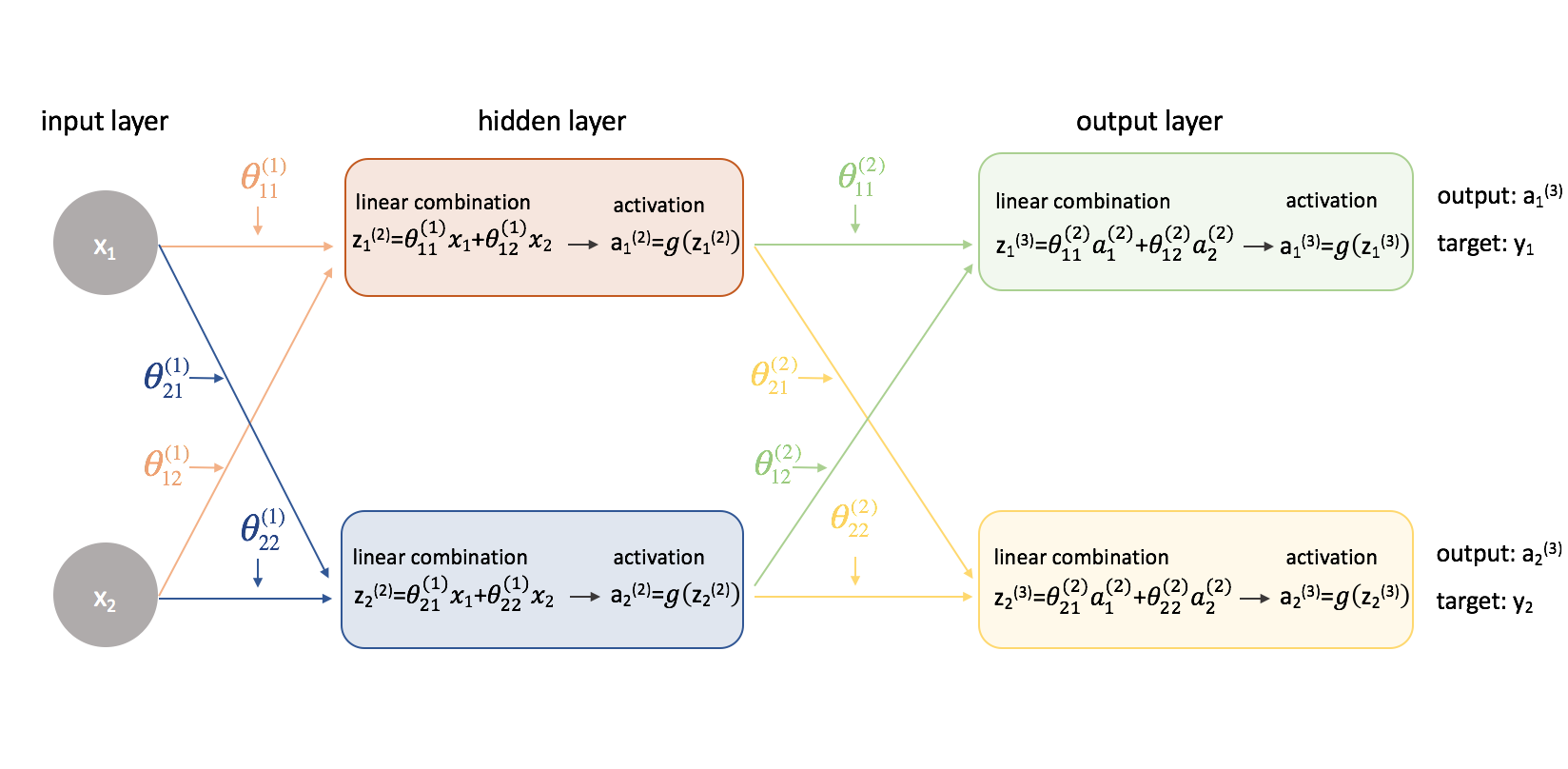
Yikes! Het is een beetje ingewikkelder geworden. Ik zal het proces doorlopen voor het vinden van een van de gedeeltelijke afgeleiden van de kostenfunctie met betrekking tot een van de parameterwaarden; de rest van de berekeningen laat ik als een oefening voor de lezer (en ik zal de eindresultaten hieronder plaatsen).

In de eerste plaats moeten we onze kostenfunctie opnieuw bekijken nu we te maken hebben met een neuraal netwerk met meer dan één uitgang. Laten we nu de gemiddelde gekwadrateerde fout als onze kostenfunctie gebruiken.

Note: Als je op meerdere waarnemingen traint (wat in de praktijk altijd het geval zal zijn), moeten we ook een optelling van de kostenfunctie over alle trainingsvoorbeelden uitvoeren. Voor deze kostenfunctie is het gebruikelijk om te normaliseren met $m$, waarbij $m$ het aantal voorbeelden in je trainingsdataset is.

Nu we onze kostenfunctie hebben gecorrigeerd, kunnen we kijken hoe het veranderen van een parameter de kostenfunctie beïnvloedt. Specifiek bereken ik in dit voorbeeld $\frac{{\left( \theta \right)}}{{\left \theta _{11}^{(1)}}}$. Als we naar het diagram kijken, beïnvloedt $theta _{11}^{(1)}$ de uitvoer voor zowel $a _1^{(3)}$ als $a _2^{(3)}$. Omdat onze kostenfunctie een optelling is van individuele kosten voor elke output, kunnen we de afgeleide keten voor elk pad berekenen en ze eenvoudigweg bij elkaar optellen.

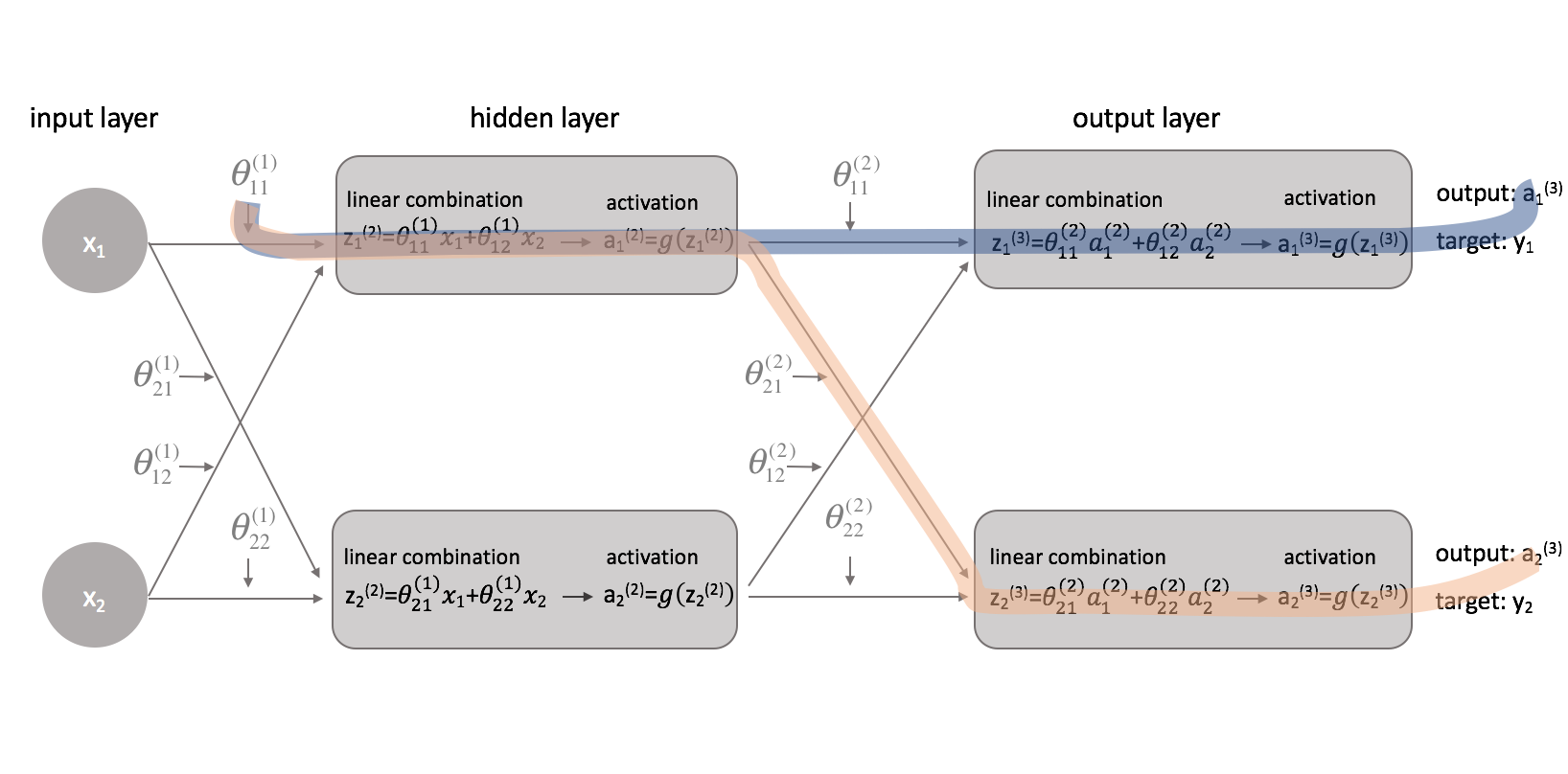
De afgeleide keten voor het blauwe pad is:
$ \left( {{\frac{\partial J\left( \theta \right)}}{{{{partial {\rm{a}}} _1^{(3)}}}} rechts)}}{\left( \theta \right)}}{\partieel {\rm{a}} _1^{(3)}}}{Deel z _1^{(3)}}}} \right)\left( {\frac{{\partiaal z _1^{(3)}}}{{\partiaal {\rm{a}}} _1^{(2)}}}} \right)\left( {\frac{{\partiaal {\rm{a}}} _1^{(2)}}}{Deel z _1^{(2)}}}} \right)\left( {{\frac{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \rechts) $

De afgeleide keten voor het oranje pad is:
$ \left( {\frac{{partiaal J\left( \theta \rechts)}}{{\partiaal {\rm{a}} _2^{(3)}}}} rechts)}}{\left( \theta \right)}}{\partieel {\rm{a}} _2^{(3)}}}{\left z _2^{(3)}}}} \right)\left( {\frac{{\partiaal z _2^{(3)}}}{{\partiaal {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\partiaal {\rm{a}}} _1^{(2)}}}{Deel z _1^{(2)}}}} \right)\left( {{\frac{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \rechts)$

Door deze te combineren krijgen we de totale uitdrukking voor ${{\frac{\partieel J_links( \theta \rechts)}}{{\partieel \theta _{11}^{(1)}}}$.

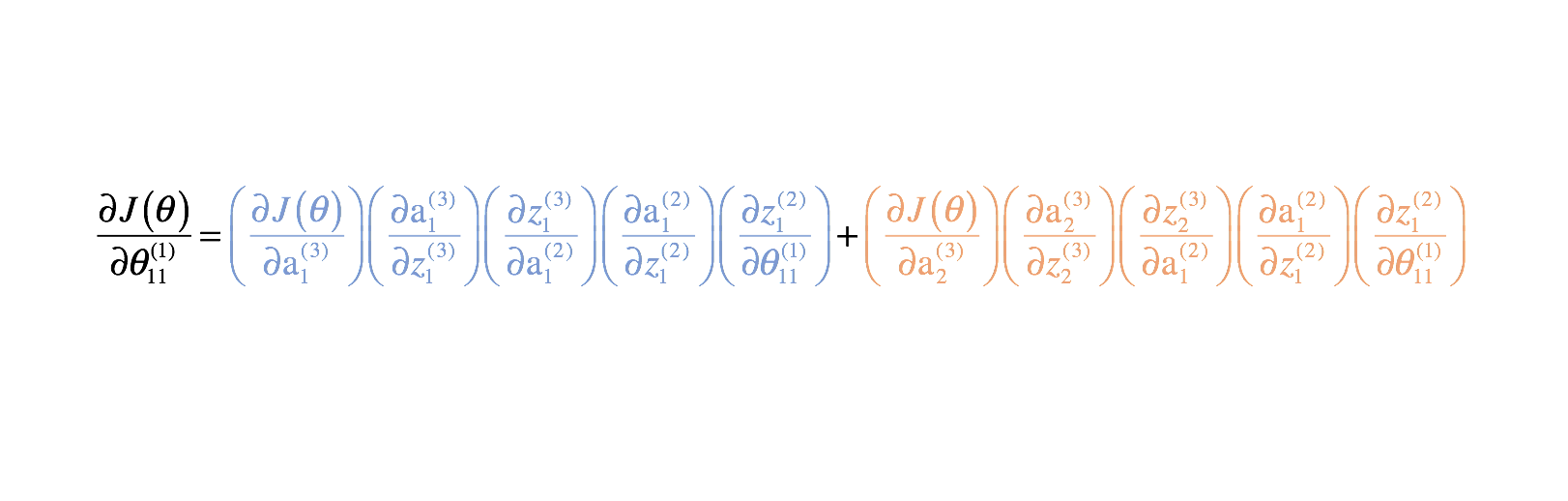
Ik heb de rest van de deelafgeleiden hieronder gegeven. Onthoud dat we deze gedeeltelijke afgeleiden nodig hebben omdat ze beschrijven hoe het veranderen van elke parameter de kostenfunctie beïnvloedt. Zo kunnen we deze kennis gebruiken om alle parameterwaarden te veranderen op een manier die de kostenfunctie blijft verlagen totdat we convergeren naar een minimumwaarde.

Laag 2 Parameters

Laag 1 Parameters

Woah daar. We zijn zojuist van een neuraal netwerk met 2 parameters die 8 gedeeltelijke afgeleide termen nodig hadden in het vorige voorbeeld, naar een neuraal netwerk met 8 parameters die 52 gedeeltelijke afgeleide termen nodig hadden. Dit loopt snel uit de hand, zeker als je bedenkt dat veel neurale netwerken die in de praktijk worden gebruikt veel groter zijn dan deze voorbeelden.

Gelukkig worden bij nadere beschouwing veel van deze partiële afgeleiden herhaald. Als we dit probleem slim aanpakken, kunnen we de computationele kosten van de training drastisch verlagen. Bovendien zou het erg vervelend zijn als we handmatig de afgeleide ketens voor elke parameter zouden moeten berekenen. Laten we eens kijken naar wat we tot nu toe hebben gedaan en of we een methode voor deze waanzin kunnen veralgemenen.

Een methode veralgemenen

Laten we de gedeeltelijke afgeleiden hierboven eens bekijken en een paar observaties doen. We beginnen met de gedeeltelijke afgeleiden te bekijken met betrekking tot de parameters voor laag 2. Vergeet niet dat de parameters voor laag 2 worden gecombineerd met de activeringen in laag 2 om als invoer in laag 3 te dienen.

Laag 2 Parameters

Laten we de volgende uitdrukkingen analyseren; ik moedig u aan om de gedeeltelijke afgeleiden gaandeweg op te lossen om uzelf van mijn logica te overtuigen.

Het lijkt er allereerst op dat de kolommen zeer vergelijkbare waarden bevatten. Zo bevat de eerste kolom gedeeltelijke afgeleiden van de kostenfunctie ten opzichte van de neurale netwerkuitgangen. In de praktijk is dit het verschil tussen de verwachte output en de werkelijke output (en dan geschaald door $m$) voor elk van de output-neuronen.

De tweede kolom vertegenwoordigt de afgeleide van de activeringsfunctie die in de outputlaag wordt gebruikt. Merk op dat voor elke laag de neuronen dezelfde activeringsfunctie zullen gebruiken. Een homogene activeringsfunctie binnen een laag is noodzakelijk om bij de berekening van de output van het neurale netwerk gebruik te kunnen maken van matrixoperaties. De waarde van de tweede kolom zal dus voor alle vier de termen gelijk zijn.

De eerste en tweede kolom kunnen voor het gemak later worden gecombineerd als $delta _i^{(3)}$. Het is niet meteen duidelijk waarom dit nuttig zou zijn, maar je zult zien als we nog een laag teruggaan waarom dit nuttig is. Mensen zullen vaak naar deze uitdrukking verwijzen als de “error” term die we gebruiken om “fouten terug te sturen van de output doorheen het netwerk”. We zullen snel zien waarom dit het geval is.

Elke neuron in het netwerk heeft een corresponderende $delta$ term die we zullen oplossen.

De derde kolom geeft aan hoe de parameter van belang verandert ten opzichte van de gewogen inputs voor de huidige laag; wanneer je de afgeleide berekent, komt dit overeen met de activering uit de vorige laag.

Ik wil ook opmerken dat de eerste twee gedeeltelijke afgeleide termen betrekking lijken te hebben op de eerste uitgangsneuron (neuron 1 in laag 3) terwijl de laatste twee gedeeltelijke afgeleide termen betrekking lijken te hebben op de tweede uitgangsneuron (neuron 2 in laag 3). Dit is duidelijk te zien in de term $ Laten we deze kennis gebruiken om de partiële afgeleiden te herschrijven met behulp van de uitdrukking $

Volgende stappen we en berekenen de laatste term van de partiële afgeleide. Zoals we hebben opgemerkt, vertegenwoordigt deze afgeleide uiteindelijk de activeringen van de vorige laag.

Note: ik vind het nuttig om de uitgebreide neurale netwerkgrafiek uit de vorige sectie te gebruiken bij het berekenen van de gedeeltelijke afgeleiden.

Het lijkt erop dat we de “fout”-termen combineren met activeringen uit de vorige laag om elke gedeeltelijke afgeleide te berekenen. Interessant is ook dat de indices $j$ en $k$ voor $\theta _{jk}$ overeenkomen met de gecombineerde indices van $\delta _j^{(3)}$ en ${\rm{a}}$

Laten we eens kijken of we een matrixbewerking kunnen bedenken om alle gedeeltelijke afgeleiden in één uitdrukking te berekenen.

$\delta ^{(3)}}$ is een vector van lengte $j$ waarbij $j$ gelijk is aan het aantal uitgangsneuronen.

δ (3) = f ′ ( a (3) )

${\rm{a}}^{(2)}$ is een vector van lengte $k$ waarbij $k$ gelijk is aan het aantal neuronen in de vorige laag. De waarden van deze vector vertegenwoordigen de activeringen van de vorige laag, berekend tijdens de voorwaartse voortplanting; met andere woorden, het is de vector van de ingangen voor de uitgangslaag.

$ {a^{(2)}} = \left $

Door deze vectoren met elkaar te vermenigvuldigen, kunnen we alle partiële afgeleide termen in één uitdrukking berekenen.

∂J( θ ) ∂ θ ij (2) ==

Om het samen te vatten, zie de grafiek hieronder.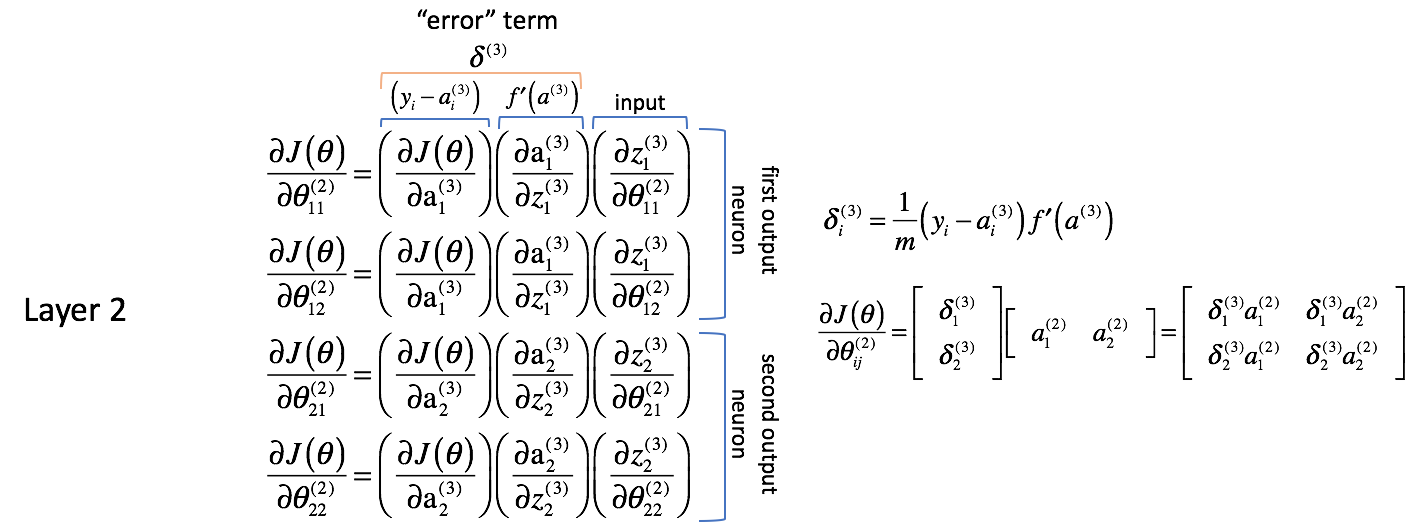

Note: Technisch gezien zou de eerste kolom ook geschaald moeten worden met $m$ om een nauwkeurige afgeleide te zijn. Mijn bedoeling was echter aan te geven dat het in deze kolom gaat om het verschil tussen de verwachte en de werkelijke output. De $delta$ term aan de rechterkant heeft de volledige afgeleide uitdrukking.

Laag 1 Parameters

Nu gaan we eens kijken wat er in laag 1 gebeurt.

Waar de gewichten in laag 2 slechts één uitgang direct beïnvloedden, beïnvloeden de gewichten in laag 1 alle uitgangen.

Hieruit volgt dat een gedeeltelijke afgeleide van de kostenfunctie met betrekking tot een parameter nu een optelling van verschillende ketens wordt. In het bijzonder hebben we een afgeleide keten voor elke $$delta$ die we in de volgende laag hebben berekend. Onthoud dat we aan het eind van het netwerk zijn begonnen en dat we door het netwerk naar achteren werken. De volgende laag voorwaarts vertegenwoordigt dus de $\delta$ waarden die we eerder hebben berekend.

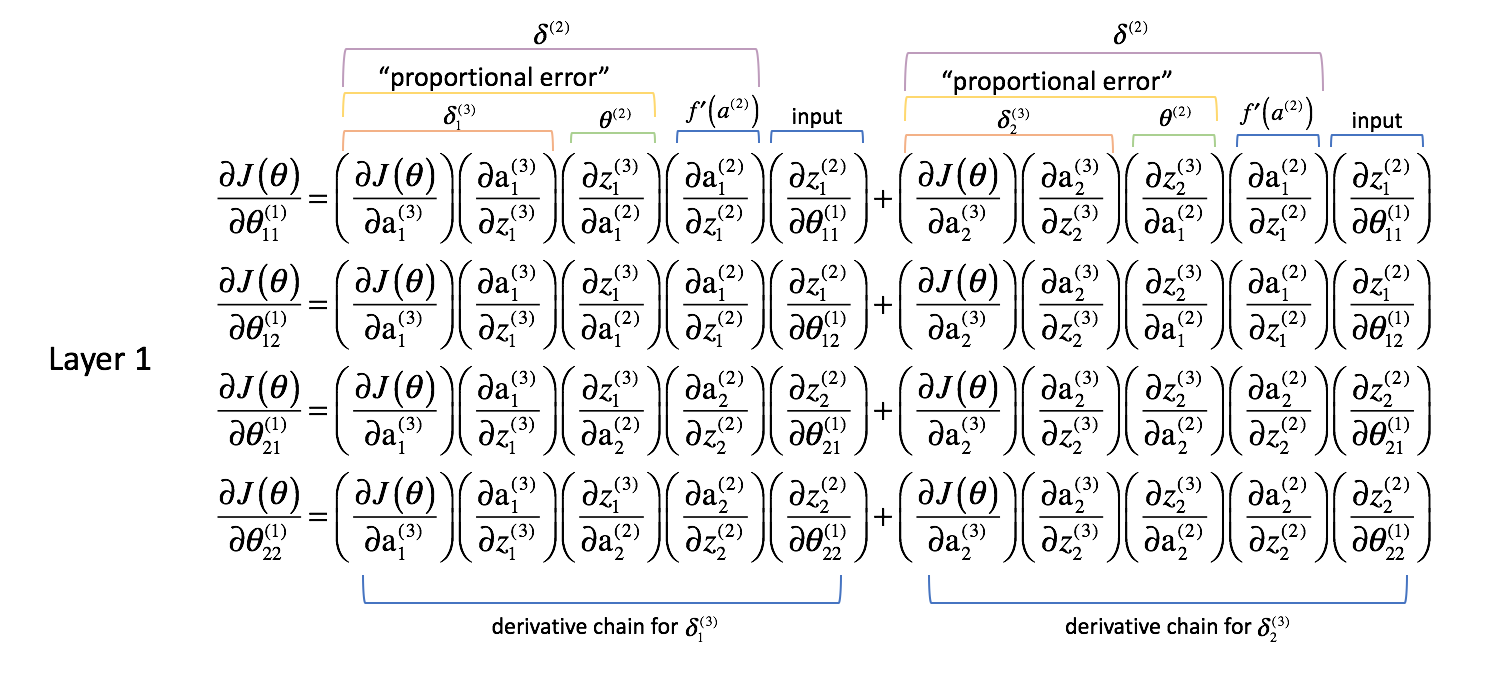
Zoals we voor laag 2 hebben gedaan, laten we een paar observaties doen.

De eerste twee kolommen (van elke bij elkaar opgetelde term) komen overeen met een $2,delta _j^{(3)}$ die in de volgende laag naar voren is berekend (denk eraan, we zijn aan het eind van het netwerk begonnen en werken nu terug).

De derde kolom komt overeen met een parameter die laag 2 met laag 3 verbindt. Als we $delta _j^{(3)}$ beschouwen als een “fout”-term voor laag 3, en elke afgeleide keten is nu een optelling van deze fouten, dan stelt deze derde kolom ons in staat om elke fout te wegen. De eerste drie termen samen vormen dus een maat voor de proportionele fout.

We herdefiniëren ook $delta$ voor alle lagen behalve de uitvoerlaag om deze combinatie van gewogen fouten op te nemen.

$ $delta _j^{(l)} = f’\left( {{a^{(l)}}} \rechts)\limits _{i = 1}^n {\delta _i^{(l + 1)}theta _{ij}^{(l)}} $

We zouden dit beknopter kunnen schrijven met behulp van matrixuitdrukkingen.

$ {\delta ^{(l)}} = {\delta ^{(l + 1)}}{Theta ^{(l)}}f’^left( {{a^{(l)}}} \rechts) $

Note: Het is standaard notatie om vectoren met kleine letters aan te duiden en matrices met hoofdletters. Zo staat $theta$ voor een vector en $theta$ voor een matrix.

De vierde kolom geeft de afgeleide weer van de activeringsfunctie die in de huidige laag wordt gebruikt. Onthoud dat de neuronen voor elke laag dezelfde activeringsfunctie gebruiken.

Ten slotte geeft de vijfde kolom de verschillende inputs van de vorige laag weer. In dit geval zijn het de eigenlijke ingangen van het neurale netwerk.

Laten we een van de termen nader bekijken, ${{\frac{{\partial J\left( \theta \right)}}{{{{partial \theta _{11}^{(1)}}}$.

Vooreerst stelden we vast dat de eerste twee kolommen van elke afgeleide keten eerder werden berekend als $\delta _j^{(3)}$.

$ \frac{{\partieel J _1^{(3)}}{{\partieel \theta _{11}^{(1)}} = \delta _1^{(3)}} {{\frac{\partieel z _1^{(3)}}{{\partieel {\rm{a}}} _1^{(2)}}}} \right)\left( {\frac{{\partiaal {\rm{a}}} _1^{(2)}}}{Deel z _1^{(2)}}}} \right)\left( {\frac{\partial z _1^{(2)}}}{\partial \theta _{11}^{(1)}}}} \rechts) + \delta _2^{(3)}left( {\frac{{\partiaal z _2^{(3)}}}{{\partiaal {\rm{a}}} _1^{(2)}}}} \right)\left( {\frac{{\partiaal {\rm{a}}} _1^{(2)}}}{Deel z _1^{(2)}}}} \right)\left( {{\frac{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \$

Verder stelden we vast dat de derde kolom van elke afgeleide keten een parameter was die elk van de respectieve $delta$ termen woog. We stelden ook vast dat de vierde kolom de afgeleide van de activeringsfunctie was.

$ \frac{{\left( \theta \right)}}}{\theta _{11}^{(1)}} = \delta _1^{(3)}{theta _{11}^{(2)}}f’\left( {{a^{(2)}}} right)}} = \delta _1^{(3)}{theta _{11}^{(2)}}f’\left( {{a^{(2)}}} \rechts)\left( {{delta _1^{(2)}}}{heta _{11}^{(1)}}}}} \rechts) + \delta _2^{(3)}theta _{21}^{(2)}f’\left( {{a^{(2)}}} \rechts)‖ {{emplarisch z _1^{(2)}}} {{emplarisch theta _{11}^{(1)}}}}}} \rechts) $

Factoring out ${\left( {{\frac{\partial z_1^{(2)}}}{\partial \theta _{11}^{(1)}}}}

$ \frac{{\partieel z _1^{(2)}}{{\partieel \theta _{11}^{(1)}}} = \left( {\frac{\partieel z _1^{(2)}}}{\partieel \theta _{11}^{(1)}}}}}} \rechts)\left( {delta _1^{(3)}theta _{11}^{(2)}f’\left( {{a^{(2)}}} \right) + \delta _2^{(3)}theta _{21}^{(2)}f’\left( {{a^{(2)}}} \$

we hebben nu onze nieuwe definitie van $delta_j^{(l)}$. Laten we dat eens invullen.

$ \frac{\partieel J_left( \theta \right)}}{\partieel \theta _{11}^{(1)}} = \left( {\frac{\partieel z _1^{(2)}}}{\partieel \theta _{11}^{(1)}}}}} \rechts)\left( {\delta _1^{(2)}}} \rechts) $

Tot slot stelden we vast dat de vijfde kolom (${{\frac{{\partieel z_1^{(2)}}}{{{\partieel \theta_{11}^{(1)}}}}$) overeenkwam met een invoer uit de vorige laag. In dit geval wordt de afgeleide berekend als $x_1$.

$ \frac{{\partial J\left( \theta_{11}^{(1)}}} = \delta _1^{(2)}{x _1} $

Ook hier weer een matrixbewerking om alle partiële afgeleiden in één uitdrukking te berekenen.

$\delta ^{(2)}$ is een vector van lengte $j$ waarbij $j$ het aantal neuronen is in de huidige laag (laag 2). We kunnen $³delta ^{(2)}$ berekenen als de gewogen combinatie van fouten uit laag 3, vermenigvuldigd met de afgeleide van de in laag 2 gebruikte activeringsfunctie.

δ (2) = f ′ ( a (2) )=

$x$ is een vector van invoerwaarden.

Door deze vectoren met elkaar te vermenigvuldigen, kunnen we alle partiële afgeleide termen in één uitdrukking berekenen.

∂J( θ ) ∂ θ ij (1) ==

Als je zo ver bent gekomen, gefeliciteerd! We hebben zojuist alle gedeeltelijke afgeleiden berekend die nodig zijn om de gradient-afdaling te gebruiken en onze parameterwaarden te optimaliseren. In de volgende sectie zal ik een manier voorstellen om het proces dat we net ontwikkeld hebben te visualiseren, naast het voorstellen van een end-to-end methode om backpropagation te implementeren.

Backpropagation

In de vorige sectie hebben we een manier ontwikkeld om alle gedeeltelijke afgeleiden te berekenen die nodig zijn voor gradient descent (gedeeltelijke afgeleide van de kostenfunctie ten opzichte van alle modelparameters) met behulp van matrix-expressies. Bij het berekenen van de gedeeltelijke afgeleiden, begonnen we aan het eind van het netwerk en werkten we, laag voor laag, terug naar het begin. We hebben ook een nieuwe term ontwikkeld, $delta$, die in wezen dient om alle gedeeltelijke afgeleide termen weer te geven die we later moeten hergebruiken en we gaan, laag voor laag, terug door het netwerk.

Note: Backpropagatie is eenvoudigweg een methode om de gedeeltelijke afgeleide van de kostenfunctie ten opzichte van alle parameters te berekenen. De eigenlijke optimalisatie van de parameters (training) geschiedt door middel van gradient descent of een andere meer geavanceerde optimalisatietechniek.

In het algemeen hebben we vastgesteld dat je de gedeeltelijke afgeleiden voor laag $l$ kunt berekenen door de $delta$ termen van de volgende laag voorwaarts te combineren met de activeringen van de huidige laag.

$ ƒrac{{\left( \theta ^{(l)}}}{\left( \theta _{ij}^{(l)}}} = {\left( {{\delta ^{(l + 1)}}} \rechts)^T}{a^{(l)}} $

Backpropagatie gevisualiseerd

Voordat ik de formele methode voor backpropagatie definieer, wil ik eerst een visualisatie van het proces geven.

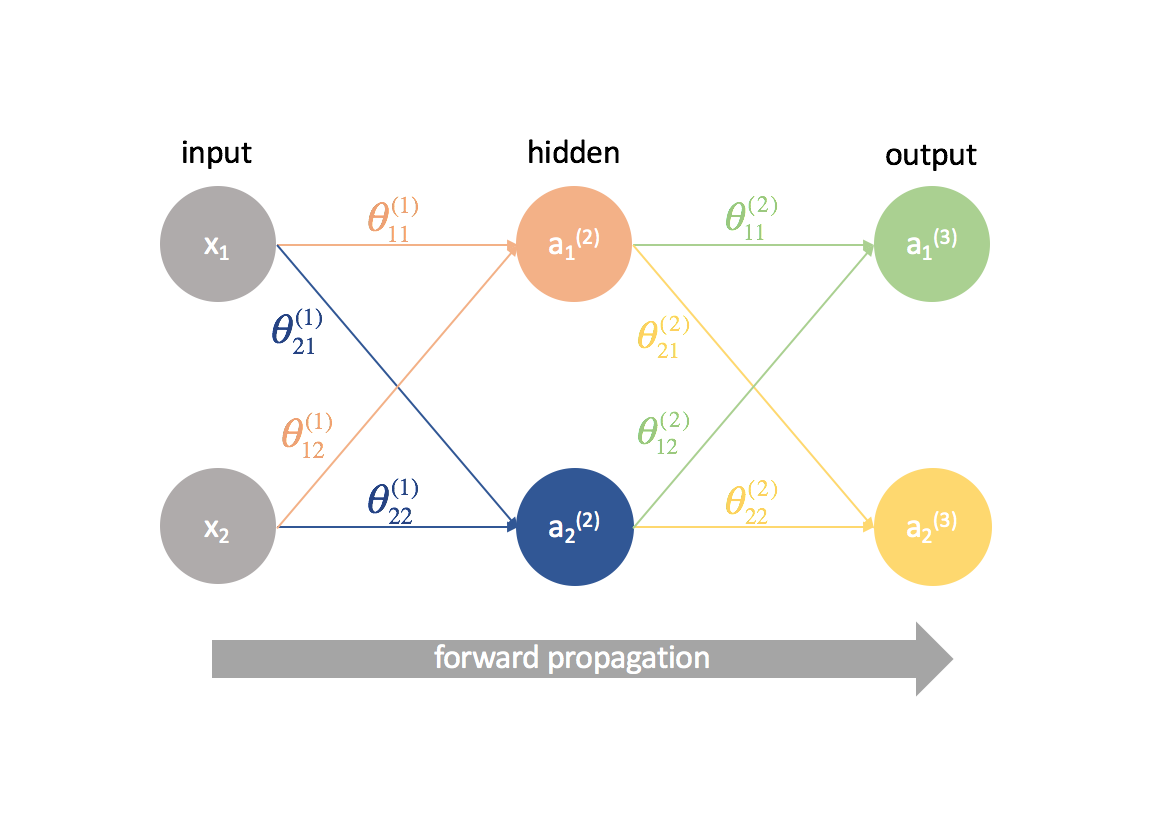
Eerst moeten we de output van een neuraal netwerk berekenen via voorwaartse propagatie.

Volgende berekenen we de ${delta ^{(3)}}$ termen voor de laatste laag in het netwerk. Onthoud dat deze $delta$ termen bestaan uit alle gedeeltelijke afgeleiden die weer gebruikt zullen worden bij het berekenen van parameters voor lagen verder terug. In de praktijk noemen we We vermenigvuldigen de fout van de derde laag met de inputs in de tweede laag om onze gedeeltelijke afgeleiden voor deze set parameters te berekenen.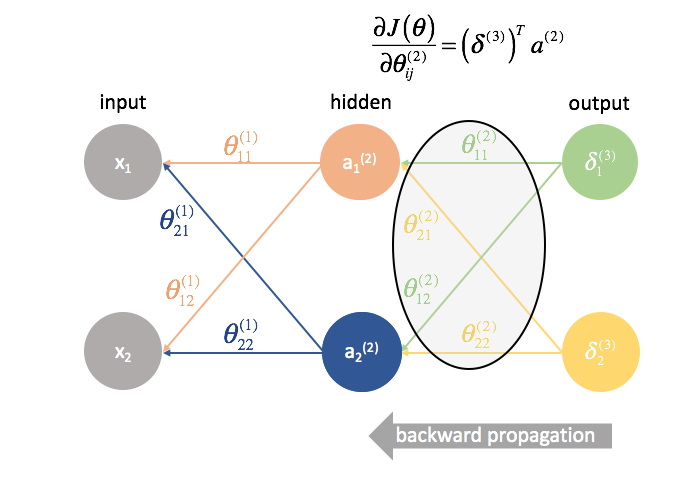

Daarna “sturen” we de “fout”-termen terug op precies dezelfde manier als we de inputs naar een neuraal netwerk “sturen”. Het enige verschil is dat we deze keer achteraan beginnen en een foutterm, laag voor laag, terugsturen door het netwerk. Vandaar de naam: backpropagatie. Het “terugsturen van onze fout” gebeurt met de uitdrukking ${{Theta ^{(3)}}{{{(2)}}$.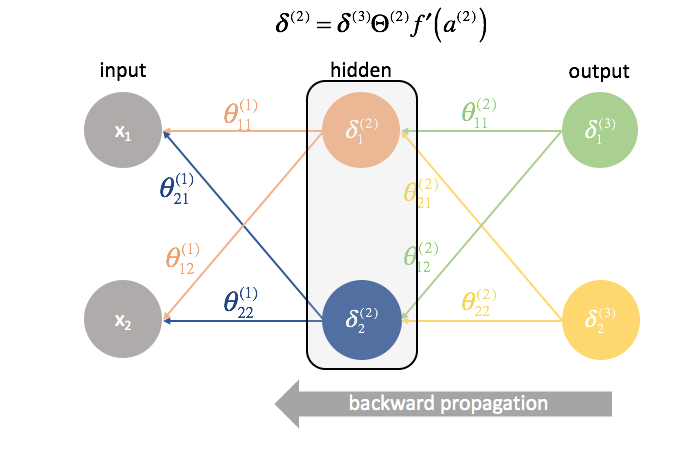

${Theta ^{(1)}}$ is de matrix van parameters die laag 1 met laag 2 verbindt. We vermenigvuldigen de fout van de tweede laag met de inputs in de eerste laag om onze gedeeltelijke afgeleiden voor deze set parameters te berekenen.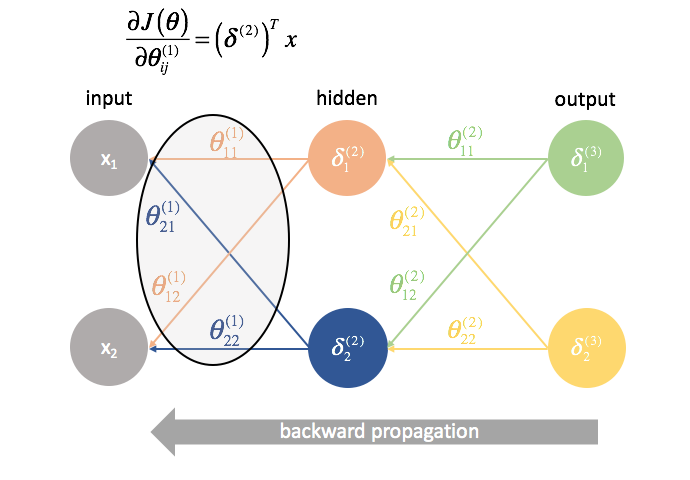

Voor elke laag, behalve de laatste, is de “fout”-term een lineaire combinatie van parameters die de verbinding vormen met de volgende laag (vooruit door het netwerk) en de “fout”-termen van die volgende laag. Dit geldt voor alle verborgen lagen, omdat we geen “fout”-term voor de ingangen berekenen.

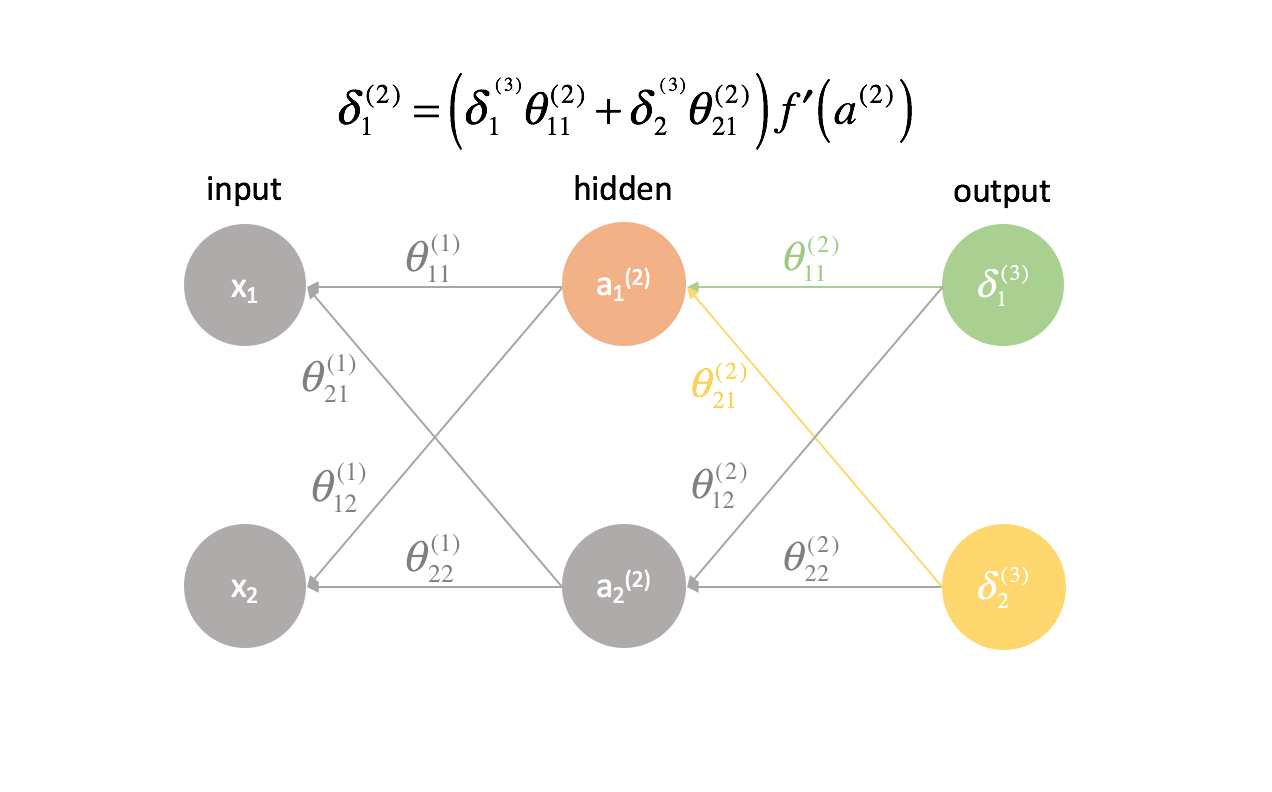
De laatste laag is een speciaal geval, omdat we de $\delta$-waarden berekenen door elke uitgangsneuron direct te vergelijken met zijn verwachte uitvoer.

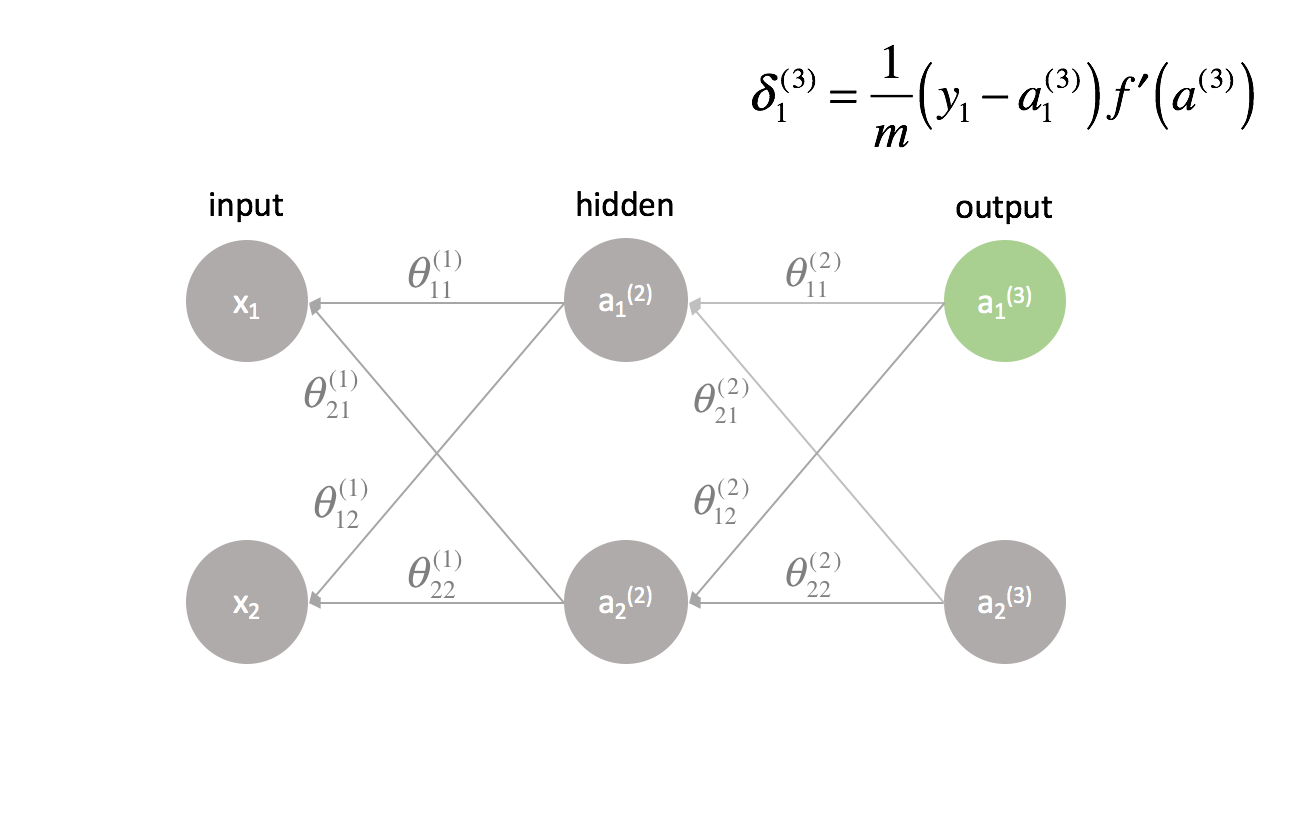
Een geformaliseerde methode voor de implementatie van backpropagation

Hiernaast presenteer ik een praktische methode voor de implementatie van backpropagation door een netwerk van lagen $l=1,2,….,L$.

1. Voer voorwaartse voortplanting uit.

2. Bereken de $delta$ term voor de uitvoerlaag.

3. Bereken de gedeeltelijke afgeleiden van de kostenfunctie met betrekking tot alle parameters die in de uitvoerlaag worden ingevoerd, ${Theta ^{(L – 1)}}$.

4. Ga één laag terug.
   $l = l – 1$

5. Bereken de $delta$ term voor de huidige verborgen laag.

6. Bereken de gedeeltelijke afgeleiden van de kostenfunctie met betrekking tot alle parameters die in de huidige laag worden ingevoerd.

7. Herhaal 4 tot en met 6 totdat je bij de inputlaag bent.

De initialisatie van de gewichten herzien

Toen we begonnen, stelde ik voor dat we onze gewichten gewoon willekeurig zouden initialiseren, zodat we een beginpunt zouden hebben. Dit stelde ons in staat om voorwaartse voortplanting uit te voeren, de uitkomsten te vergelijken met de verwachte waarden en de kosten van ons model te berekenen.

Het is eigenlijk heel belangrijk dat we onze gewichten op willekeurige waarden initialiseren, zodat we de symmetrie in ons model kunnen doorbreken. Als we al onze gewichten gelijk hadden geïnitialiseerd, zou elk neuron in de volgende laag gelijk zijn aan dezelfde lineaire combinatie van waarden.

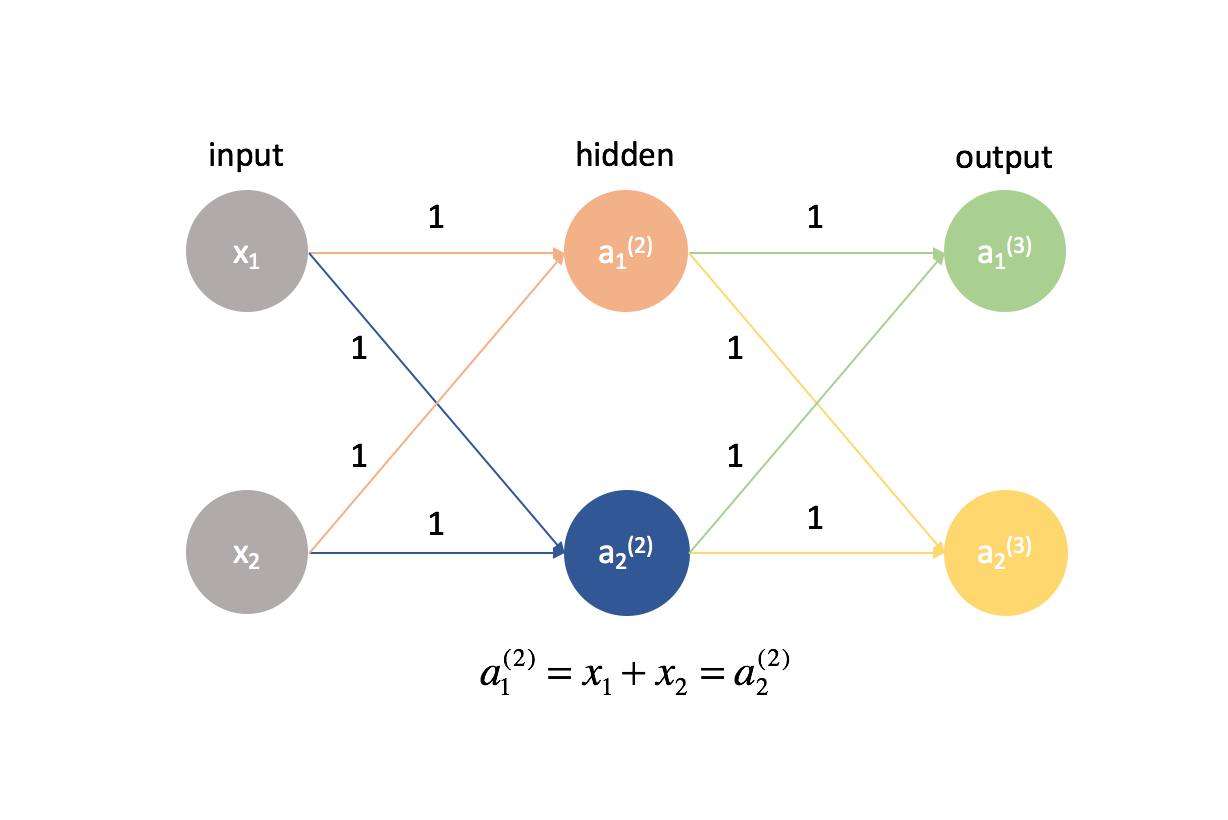
Volgens dezelfde logica zouden de $delta$ waarden ook gelijk zijn voor elk neuron in een bepaalde laag.

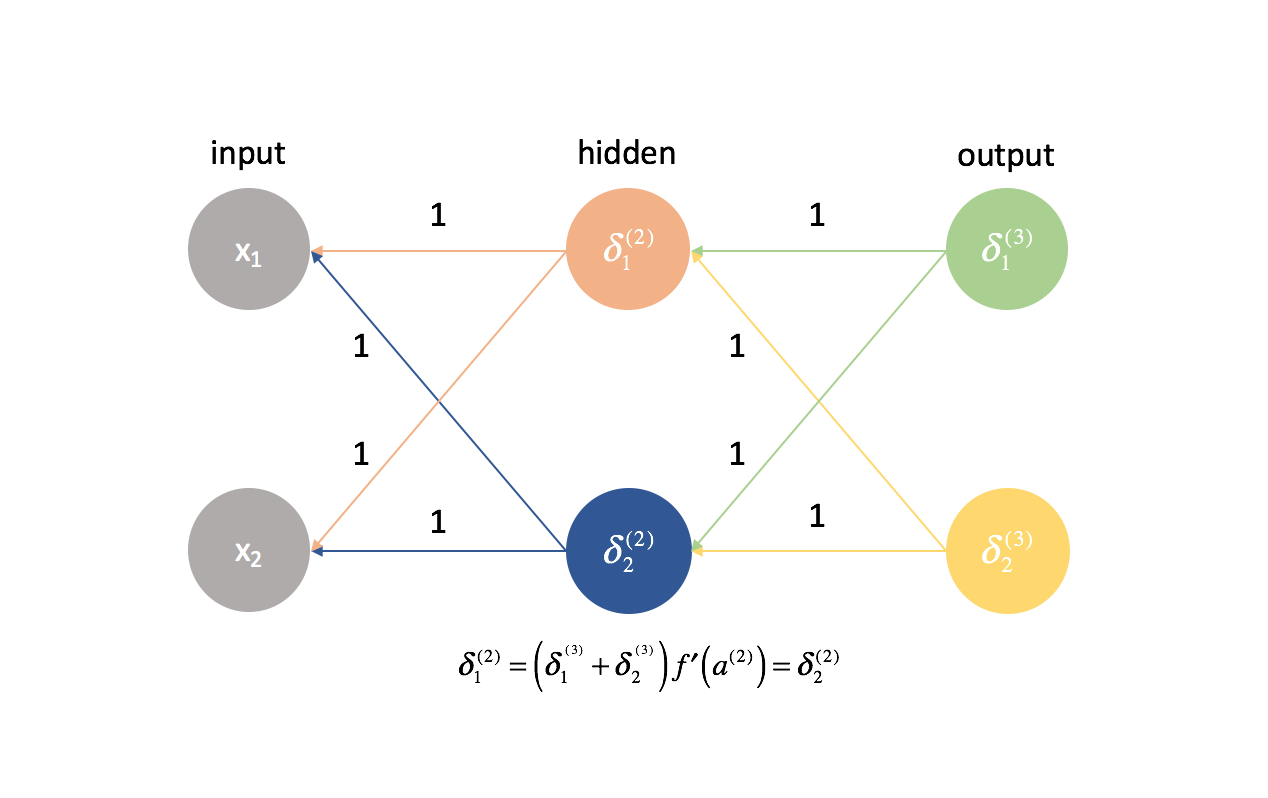
Daarnaast, omdat we de gedeeltelijke afgeleiden in een bepaalde laag berekenen door de $$delta$ waarden en de activeringen te combineren, zouden alle gedeeltelijke afgeleiden in een bepaalde laag identiek zijn. Op die manier zouden de gewichten symmetrisch bijgewerkt worden in de gradiënt-afdaling en zouden meerdere neuronen in een laag nutteloos zijn.

Door de gewichten van het netwerk willekeurig te initialiseren, kunnen we deze symmetrie doorbreken en elk gewicht afzonderlijk bijwerken op basis van zijn relatie met de kostenfunctie. Normaal gesproken geven we elke parameter een willekeurige waarde in $\left$ waarbij $\varepsilon$ een waarde dicht bij nul is.

Het geheel samenvoegen

Als we alle partiële afgeleiden voor de parameters van het neurale netwerk hebben berekend, kunnen we gradiëntafdaling gebruiken om de gewichten bij te werken.

In het algemeen definiëren we de gradiënt-afdaling als

waarbij $\Delta {\theta _i}$ de “stap” is die we langs de gradiënt nemen, geschaald door een leersnelheid, $\eta$.

We gebruiken deze formule om elk van de gewichten bij te werken, de voorwaartse voortplanting met de nieuwe gewichten opnieuw te berekenen, de fout terug te propageren, en de volgende gewichtupdate te berekenen. Dit proces gaat door totdat we geconvergeerd zijn op een optimale waarde voor onze parameters.

Tijdens elke iteratie voeren we forward propagation uit om de outputs te berekenen en backward propagation om de fouten te berekenen; een volledige iteratie staat bekend als een epoch. Het is gebruikelijk om na elke epoch evaluatiemetingen te rapporteren, zodat we de evolutie van ons neurale netwerk kunnen volgen terwijl het traint.

Verder lezen

• The Matrix Calculus You Need For Deep Learning

• Hoe het backpropagation-algoritme werkt

• Stanford cs231n: Backpropagatie, Intuïties

• CS231n Winter 2016: Lezing 4: Backpropagation, Neurale Netwerken 1

• Lessen over Deep Learning

• Ja je moet backprop begrijpen

• Bouwstenen van neurale netwerken

• En voor het geval je het net hebt opgegeven over backpropagation…. Deep Learning zonder backpropagatie

delta$ meestal de “fout”-term.

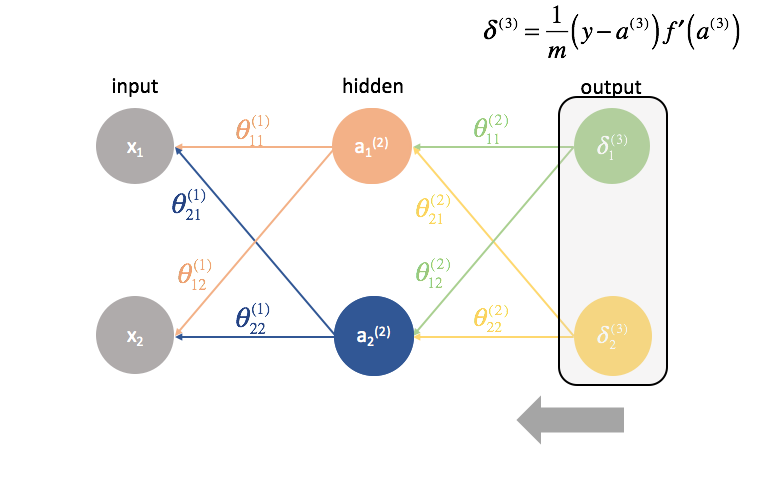
${Theta ^{(2)}}$ is de matrix van parameters die laag 2 met 3 verbindt. We multiply the error from the third layer by the inputs in the second layer to calculate our partial derivatives for this set of parameters.

Next, we “send back” the “error” terms in the exact same manner that we “send forward” the inputs to a neural network. The only difference is that time, we’re starting from the back and we’re feeding an error term, layer by layer, backwards through the network. Hence the name: backpropagation. The act of “sending back our error” is accomplished via the expression ${\delta ^{(3)}}{\Theta ^{(2)}}$.

${\Theta ^{(1)}}$ is the matrix of parameters that connects layer 1 to 2. We multiply the error from the second layer by the inputs in the first layer to calculate our partial derivatives for this set of parameters.

For every layer except for the last, the “error” term is a linear combination of parameters connecting to the next layer (moving forward through the network) and the “error” terms of that next layer. This is true for all of the hidden layers, since we don’t compute an “error” term for the inputs.

The last layer is a special case because we calculate the $\delta$ values by directly comparing each output neuron to its expected output.

A formalized method for implementing backpropagation

Here, I’ll present a practical method for implementing backpropagation through a network of layers $l=1,2,…,L$.

1. Perform forward propagation.

2. Compute the $\delta$ term for the output layer.

3. Compute the partial derivatives of the cost function with respect to all of the parameters that feed into the output layer, ${\Theta ^{(L – 1)}}$.

4. Go back one layer.
   $l = l – 1$

5. Compute the $\delta$ term for the current hidden layer.

6. Compute the partial derivatives of the cost function with respect to all of the parameters that feed into the current layer.

7. Repeat 4 through 6 until you reach the input layer.

Revisiting the weights initialization

When we started, I proposed that we just randomly initialize our weights in order to have a place to start. This allowed us to perform forward propagation, compare the outputs to the expected values, and compute the cost of our model.

It’s actually very important that we initialize our weights to random values so that we can break the symmetry in our model. If we had initialized all of our weights to be equal to be the same, every neuron in the next layer forward would be equal to the same linear combination of values.

By this same logic, the $\delta$ values would also be the same for every neuron in a given layer.

Further, because we calculate the partial derivatives in any given layer by combining $\delta$ values and activations, all of the partial derivatives in any given layer would be identical. As such, the weights would update symmetrically in gradient descent and multiple neurons in any layer would be useless. This obviously would not be a very helpful neural network.

Randomly initializing the network’s weights allows us to break this symmetry and update each weight individually according to its relationship with the cost function. Typically we’ll assign each parameter to a random value in $\left$ where $\varepsilon$ is some value close to zero.

Putting it all together

After we’ve calculated all of the partial derivatives for the neural network parameters, we can use gradient descent to update the weights.

In general, we defined gradient descent as

where $\Delta {\theta _i}$ is the “step” we take walking along the gradient, scaled by a learning rate, $\eta$.

We’ll use this formula to update each of the weights, recompute forward propagation with the new weights, backpropagate the error, and calculate the next weight update. This process continues until we’ve converged on an optimal value for our parameters.

During each iteration we perform forward propagation to compute the outputs and backward propagation to compute the errors; one complete iteration is known as an epoch. It is common to report evaluation metrics after each epoch so that we can watch the evolution of our neural network as it trains.

Further reading

• The Matrix Calculus You Need For Deep Learning

• How the backpropagation algorithm works

• Stanford cs231n: Backpropagation, Intuitions

• CS231n Winter 2016: Lecture 4: Backpropagation, Neural Networks 1

• Lectures on Deep Learning

• Yes you should understand backprop

• Building blocks of neural networks

• And in case you just gave up on backpropagation… Deep Learning without Backpropagation