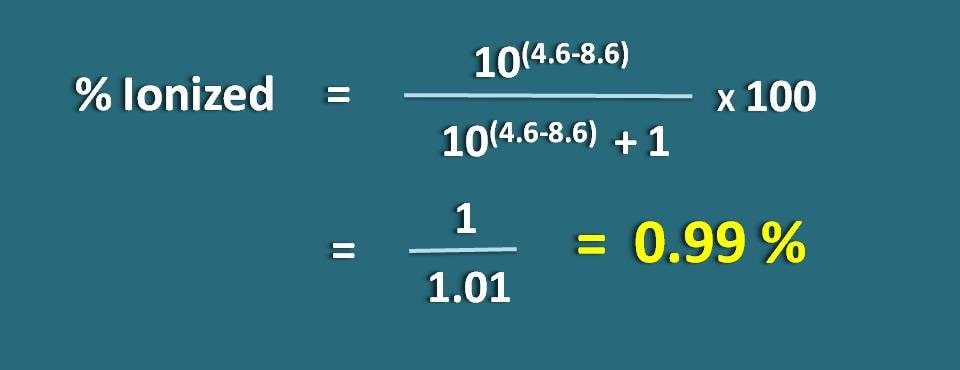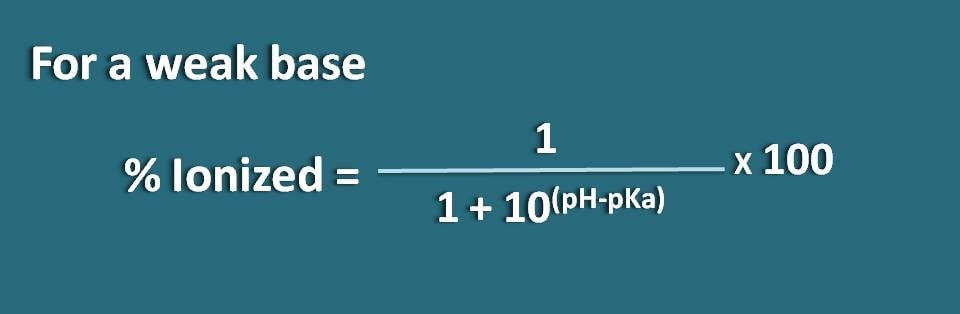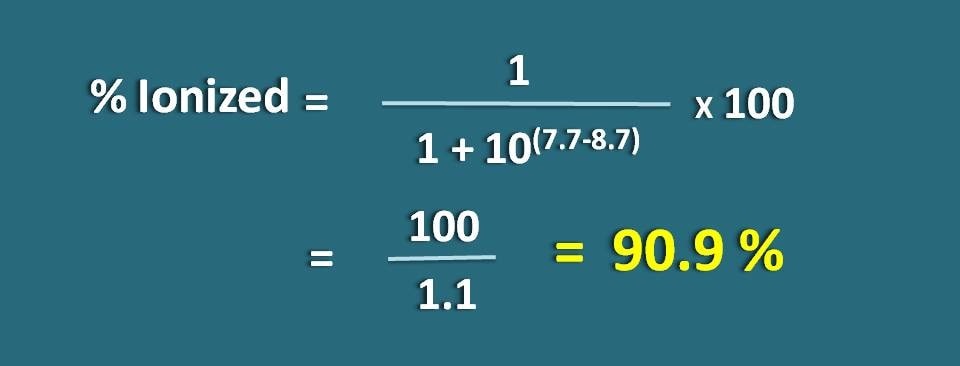Soms moeten we de ionisatiestatus van een organische verbinding kennen om enkele fysisch-chemische eigenschappen van die verbinding te kunnen beoordelen. Als de verbinding bijvoorbeeld meer geïoniseerd is bij een bepaalde pH, zal zij beter oplosbaar zijn in water. Aan de andere kant, als we ons concentreren op de permeabiliteit van de verbinding over een fysiologisch membraan, dan is de geünioniseerde vorm van de verbinding belangrijker, omdat deze meer lipofiel is en het lipofiele membraan kan passeren.
Berekening van het ionisatiepercentage is dus een essentiële taak die we vaak tegenkomen als we te maken hebben met de farmacokinetica van geneesmiddelen. Laten we hier eens kijken hoe we het kunnen berekenen, samen met een paar voorbeelden.
Henderson-Hasselbalch-vergelijking
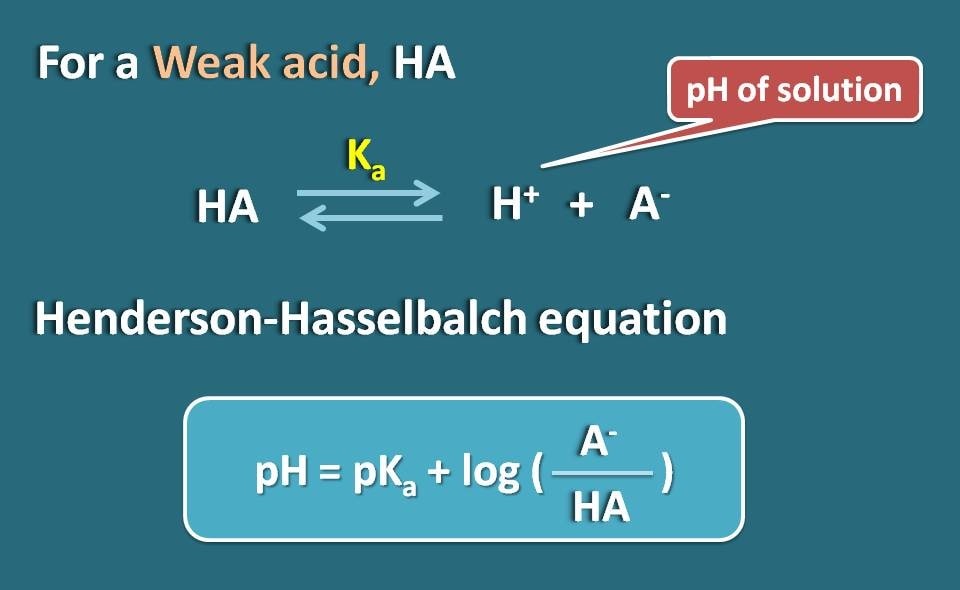
Laten we een zwakke elektrolyt nemen zoals HA, dat zich gedraagt als een zwak zuur. Wanneer het in water is opgelost, is het niet volledig geïoniseerd, maar bereikt het een evenwicht zodat het zowel in geïoniseerde als in geünioniseerde vorm kan bestaan.
Door Hendersen-Hasselbach-vergelijking voor het zwakke zuur toe te passen, kunnen we de pH van de oplossing in verband brengen met de pKa van het geneesmiddel en de ionisatie ervan.
Dus, pH=pKa + log(A-/HA)
Waarbij A- de geïoniseerde vorm van het zwakke zuur is, terwijl HA de geünioniseerde vorm is.
Laten we nu deze vergelijking herschikken zodat we de verhouding krijgen tussen de geïoniseerde en de geünioniseerde vormen van het zwakke zuur.
log(A-/HA)=pH – pKa
Door de antilogaritme te nemen,
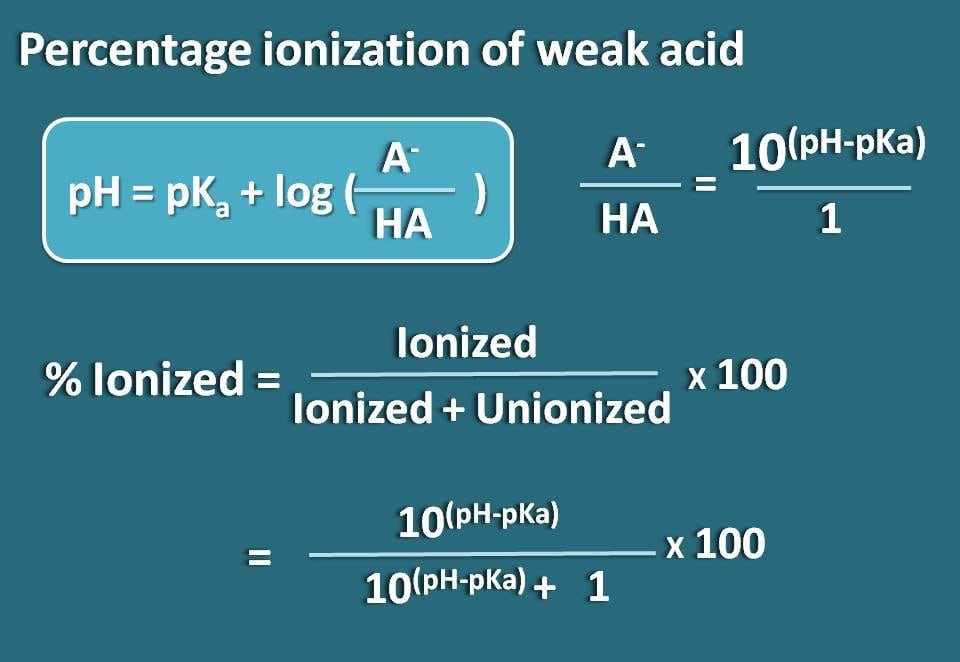
A-/HA=10(pH – pKa)
Nu weten we de verhouding tussen de geïoniseerde vorm en de gebonden vorm. Hieruit kunnen we het ionisatiepercentage berekenen.
% geïoniseerd= * 100
Subiteren in deze vergelijking,
% geïoniseerd=* 100
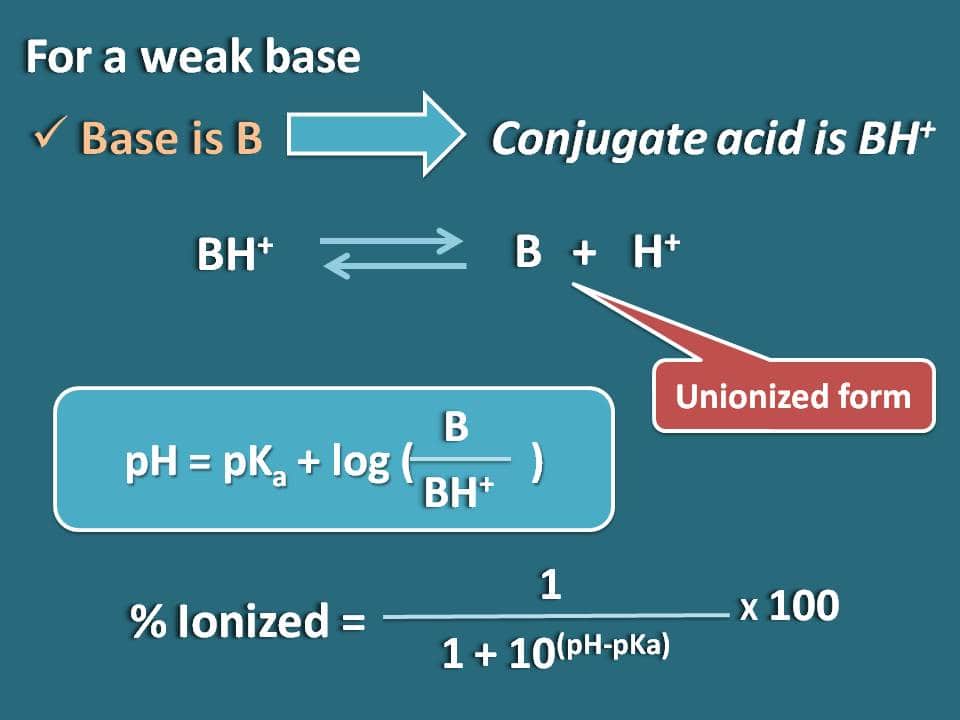
Op soortgelijke wijze kunnen we de formule verkrijgen voor een zwakke base als B waarvan het geconjugeerde zuur BH+ is. Nu kunnen we het chemisch evenwicht voor het geconjugeerde zuur schrijven zoals hieronder.
Nu schrijven we de Hendersen-Hasselbalch vergelijking voor het geconjugeerde zuur
pH=pKa + log (B/BH+)
Nu kan de verhouding tussen de verenigde en geïoniseerde vormen van de base worden geschreven als
B/BH+=10(pH – pKa)
Hier is het aandeel van de verenigde vorm 10(pH – pKa) terwijl dat van de geïoniseerde vorm 1 is. Dus het ionisatiepercentage wordt
% geïoniseerd=* 100
Aternatief, kunnen we ook de bovenstaande vergelijking herschikken door de term pH-pKa om te keren in pKa-pH waarbij we de formule krijgen als
% geïoniseerd=* 100
Nu gaan we naar enkele praktijkvoorbeelden en laten we eens kijken hoe we deze kunnen oplossen.
Werkvoorbeeld 1
Bereken het geïoniseerde percentage van een zwak zuur geneesmiddel bij een pH van 4,6 met een pKa-waarde van 8,6.
Oplossing:
Laten we eerst de gegeven gegevens op een rijtje zetten.
pH=4,6 en pKa=8,6
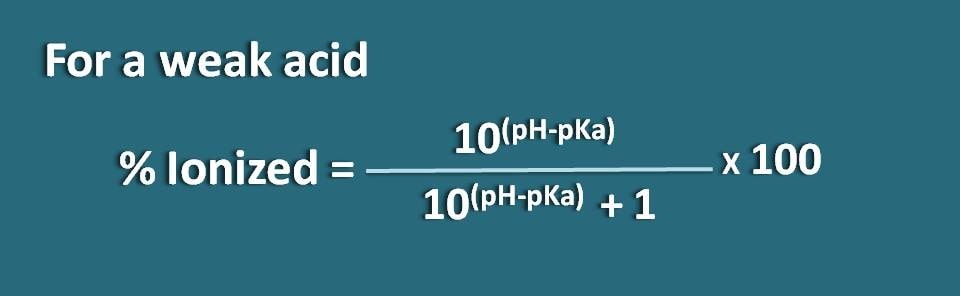
Omdat het een zwak zuur geneesmiddel is, laten we de volgende formule toepassen.
Substitueren in bovenstaande vergelijking,
% geïoniseerd=* 100
=1/1,01=0.99 %
Laten we een ander voorbeeld nemen.
Werkvoorbeeld 2
Bereken de fractie van het geneesmiddel in de geïoniseerde vorm bij pH 7.7 van een weefsel voor een basisch geneesmiddel met pKa 8,7.
Oplossing:
Laten we eerst de gegeven gegevens op een rij zetten.
pH=7.7 en pKa=8.7
Hier is sprake van een zwakke base, dus moeten we de volgende formule toepassen.
Substitueren in bovenstaande vergelijking,
% geïoniseerd=* 100
=100/1.1=90,9 %
Tot slot sluiten we af met een ander voorbeeld.
Werkvoorbeeld 3
Bereken de verhouding tussen geprotoneerde en ongeprotoneerde vormen van morfine bij pH 5. De pKa van morfine is 7.
Oplossing:
Ook hier is de gegeven datum pH=5 en pKa=7.
Morfine is een opioïde analgeticum dat tertiair amine in de ring heeft en daardoor als zwakke base fungeert. Maar hier werd gevraagd naar de verhouding tussen geprotoneerde en ongeprotoneerde vormen van het geneesmiddel. De geprotoneerde vorm is niets anders dan de geïoniseerde vorm, terwijl de ongeprotoneerde vorm de geünioniseerde vorm is. Voor een zwakke base zal de verhouding 10(pH – pKa) : 1 zijn.
en laten we de waarden substitueren.
Geprotoneerd/ongeprotoneerd=10(5 – 7)/1